
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КРАТНЫЕ ИНТЕГРАЛЫ. Двойной интеграл в полярных координатах
КРАТНЫЕ ИНТЕГРАЛЫ
Двойной интеграл в прямоугольных координатах
Пусть в ограниченной замкнутой области D на плоскости Oxy определена непрерывная функция z = f(x,y). Разобьем область D на n областей с площадями DSi , в каждой из них выберем произвольную точку ( xi , yi ) и составим интегральную сумму 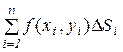 . Предел этой суммы при неограниченном увеличении числа областей разбиения и при стремлении диаметра наибольшей области max di к нулю называется двойным интегралом от функции z = f(x,y) по области D :
. Предел этой суммы при неограниченном увеличении числа областей разбиения и при стремлении диаметра наибольшей области max di к нулю называется двойным интегралом от функции z = f(x,y) по области D :
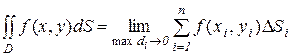 .
.
Элементарная площадь dS в декартовых координатах dS = dxdy`.
Для вычисления двойного интеграла важное значение имеет вид области D.
a) б)

 y y
y y

 y=j2(x) I II
y=j2(x) I II

 d
d
 | |||
 | |||
|

|
 | |||
 | |||
0 a в x 0 x
Рис. 1.
Если область D может быть задана так, как показано на рис.1.а, двойной интеграл вычисляется по формуле
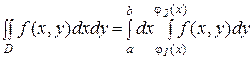 . ( 1 )
. ( 1 )
Если область D имеет вид такой, как показано на рис.1.б, двойной интеграл вычисляется по формуле
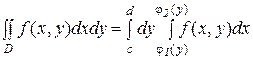 ( 2 )
( 2 )
В более сложных случаях область D разбивают на простые области типа I и II и пользуются свойством аддитивности двойного интеграла:
если D = D1 + D2 , то 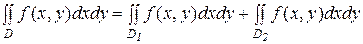 .
.
Двойной интеграл в полярных координатах
Переход от прямоугольных декартовых координат к полярным выполняется по формулам
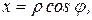
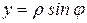 ,
, 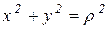 ( 3 )
( 3 )
при условии, что полюс помещен в начале координат и полярная ось направлена вдоль оси Ox . Элемент площади в полярных координатах имеет вид:
dS = rdrdj.
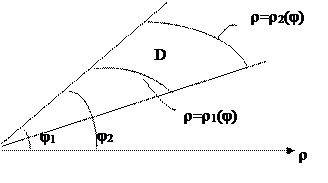 |
Рис. 2.
Если область D задана так, как показано на рис.2 ( j1 £ j £ j2, , r1(j) £ r £ r2(j) ), то переход к полярным координатам в двойном интеграле выполняется по формуле:
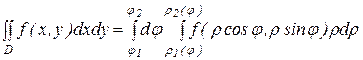 . ( 4 )
. ( 4 )
Если область D охватывает начало координат, в ( 4 ) надо положить r1(j) = 0 .
Приложения двойных интегралов
Площадь плоской области D на плоскости Oxy вычисляется по формуле:
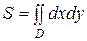 . ( 5 )
. ( 5 )
Если D - плоская пластинка, лежащая в плоскости Oxy, с поверхностной плотностью 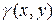 , то массу пластинки находят по формуле
, то массу пластинки находят по формуле
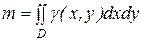 . ( 6 )
. ( 6 )
Пример 1: С помощью двойного интеграла вычислить площадь области, ограниченной линиями y = x2 - 1 и y = 2.
|
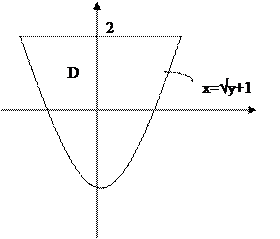 |
-1 0 1 x
Pис. 3.
Спроектируем область D на ось Oy и воспользуемся для вычисления
двойного интеграла формулой (13):
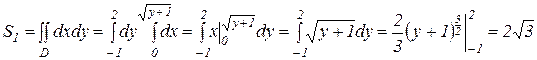 .
.
Тогда площадь всей области D равна S = 2S1 =4 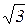 .
.
Ответ: S = 4 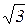 .
.
g
Пример 2. Вычислить площадь плоской области, ограниченной кривой 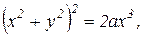
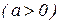 .
.
Решение: Введем полярные координаты ( 14 ), тогда уравнение кривой примет вид 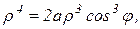 или
или 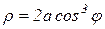 .
.
Область D показана на рис. 4.
 y
y
|

 |
|
Рис. 4.
Эта область симметрична относительно оси , поэтому достаточно вычислить площадь верхней половины области D и результат удвоить. Для верхней половины угол j меняется от 0 до p / 2, а r меняется от 0 до 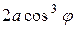 ,
,
поэтомy
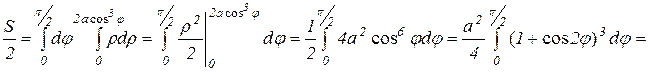
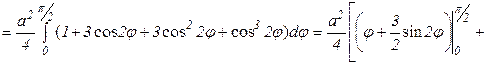
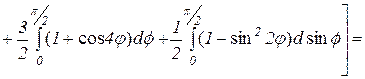
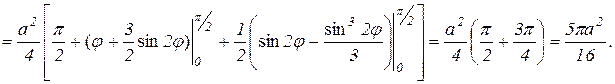

Ответ: Площадь всей области 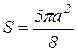 (кв.ед.).
(кв.ед.).
g
Пример 3: С помощью двойного интеграла вычислить массу плоской пластинки, ограниченной линиями 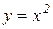 ,
, 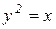 , с заданной плотностью
, с заданной плотностью 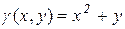 .
.
Решение: Построим область D (рис.6).
 |
D
| |
Рис. 5
Эта область ограничена двумя параболами. Проекцией области на ось Ох является отрезок [ 0 ; 1 ]. Массу пластинки найдем по формуле (17), вычисляя
двойной интеграл по формуле (1):
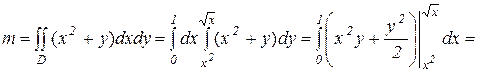
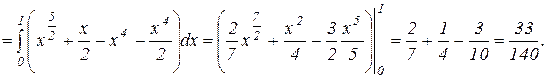
Ответ: 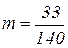 ед. массы.
ед. массы.
g
Пример 4. Вычислить массу плоской пластинки, ограниченной линиями
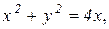
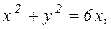
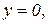
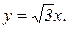
Поверхностная плотность 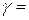
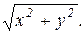

Решение: Построим область D. Уравнение 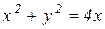 является уравнением окружности
является уравнением окружности 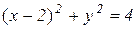 с центром в точке (2; 0) и радиусом 2 . Уравнение
с центром в точке (2; 0) и радиусом 2 . Уравнение 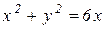 является уравнением окружности
является уравнением окружности 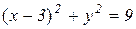 с центром в точке (3; 0) и радиусом 3 . Уравнения
с центром в точке (3; 0) и радиусом 3 . Уравнения 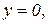
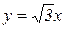 задают прямые линии (см. рис.6).
задают прямые линии (см. рис.6).
При вычислении массы пластинки по формуле (6) перейдем к полярным координатам (3). Тогда уравнения границ области D примут вид:
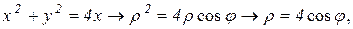
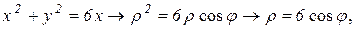
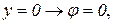
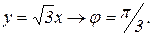
Поверхностная плотность в полярных координатах 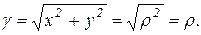


| |
|

|
|
|

|
|
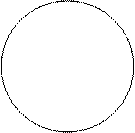
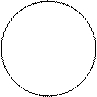
Рис.6
Тогда масса пластинки равна
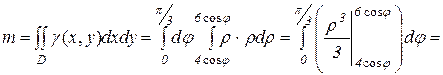
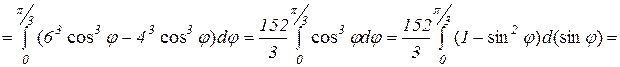

Oтвет: 19 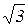 ед. массы.
ед. массы.
Тройной интеграл в прямоугольных координатах
Пусть в области V, заданной в пространстве и ограниченной замкнутой поверхностью S, определена непрерывная функция f(x,y,z) .Разобьем область V на n частичных областей ΔVi , в каждой области выберем произвольную точку (xi,yi,zi)и составим интегральную сумму 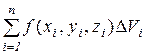 . Предел этих сумм при неограниченном увеличении числа областей разбиения n и при стремлении к нулю диаметра наибольшей области max di называется тройным интегралом от функции f(x,y,z) по области V :
. Предел этих сумм при неограниченном увеличении числа областей разбиения n и при стремлении к нулю диаметра наибольшей области max di называется тройным интегралом от функции f(x,y,z) по области V :
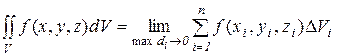 .
.
В декартовых координатах элемент объема dV=dxdydz.
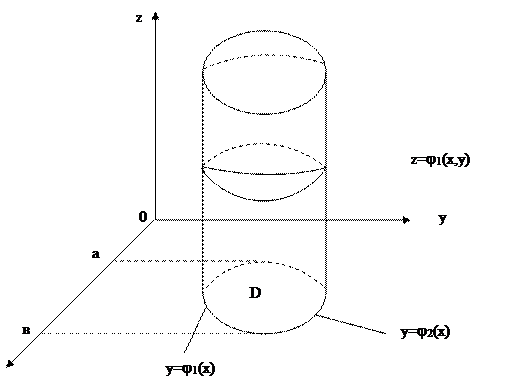 |
|
|
Рис. 7.
Пусть пространственная область V проектируется в область D на плоскости Oxy и ограничена снизу поверхностью 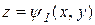 , сверху — поверхностью
, сверху — поверхностью 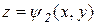 , а с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. (см. рис. 7). В этом случае тройной интеграл вычисляется по формуле
, а с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. (см. рис. 7). В этом случае тройной интеграл вычисляется по формуле
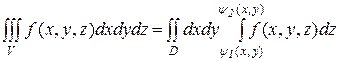 (7) или
(7) или
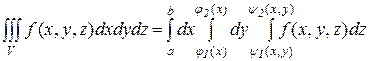 (7΄)
(7΄)
В формулах (18) и (18') возможно изменить порядок интегрирования, проектируя область D в какую-либо другую координатную плоскость.
Тройной интеграл в цилиндрических и сферических координатах
 |
x
Рис. 8.
Декартовы координаты точки M(x,y,z) связаны с цилиндрическими координатами j, r, z соотношениями:
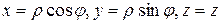 , (8)
, (8)
где 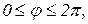
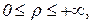
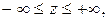 причем
причем 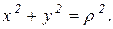
Cвязь между декартовыми и сферическими координатами j, q, r точки имеет вид:
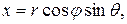
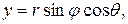
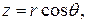 (9)
(9)
где 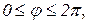
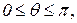
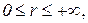 причем
причем 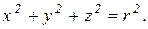
Переход в тройном интеграле к цилиндрическим координатам осуществляется по формуле:
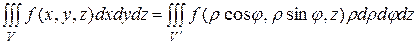 , (10)
, (10)
где V¢ - область изменения цилиндрических координат, соответствующая объему V .
Переход в тройном интеграле к сферическим координатам выполняется по формуле:
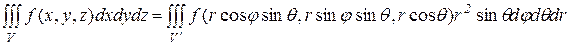 , (11) где V¢ - область изменения сферических координат, соответствующая объему V.
, (11) где V¢ - область изменения сферических координат, соответствующая объему V.
Приложения тройного интеграла
Объем пространственного тела V находится по формулам:
в прямоугольных координатах: 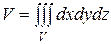 , (12)
, (12)
в цилиндрических координатах: 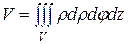 (13)
(13)
и в сферических координатах: 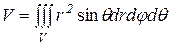 . (14)
. (14)
Масса тела с плотностью 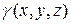 , занимающего пространственную область V , находится по формуле
, занимающего пространственную область V , находится по формуле
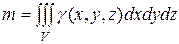 , (15)
, (15)
в которой при необходимости можно перейти к цилиндрическим или cферическим координатам в соответствии с (10) и (11).
Пример 5. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: 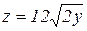 ,
, 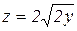 , z = 0, z + y=0.5. Сделать чертеж тела и его проекции в плоскость Oxy.
, z = 0, z + y=0.5. Сделать чертеж тела и его проекции в плоскость Oxy.
Решение: Тело ограничено снизу плоскостью Oxy (z = 0), сверху — плоскостью z + y = 0.5, параллельной оси Oz. Боковая поверхность образована двумя цилиндрическими поверхностями (см. рис. 10).
Объем тела вычисляется по формуле (18):
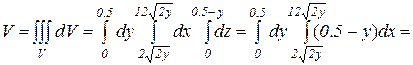
|

| |










|
|
|


|
|



|
|
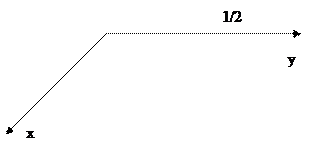 | |||
 | |||
Рис.9
= 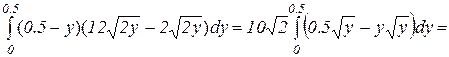
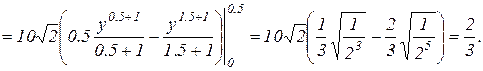
Ответ: V = 2/3 (ед.3).
g
Пример 6. Найти объем тела, ограниченного поверхностями 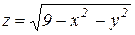 ,
, 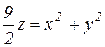 . Сделать чертеж тела и его проекции в плоскость Oxy.
. Сделать чертеж тела и его проекции в плоскость Oxy.
Решение: Тело ограничено снизу поверхностью параболоида с вершиной в начале координат ( 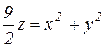 ), сверху – полусферой радиусом 3 (
), сверху – полусферой радиусом 3 ( 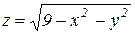 ). Проекцией тела в плоскость Оху является круг с центром в начале координат, радиус которого можно найти, исключая z из уравнения параболоида. Получим
). Проекцией тела в плоскость Оху является круг с центром в начале координат, радиус которого можно найти, исключая z из уравнения параболоида. Получим 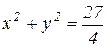 .
.
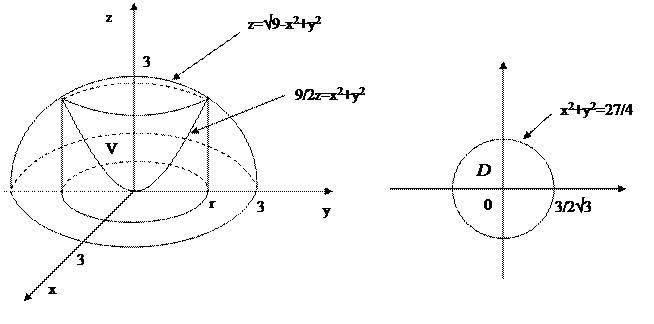
|
|
Рис. 10.
Объем тела V удобно вычислить в цилиндрических координатах по формуле (24). В этом случае уравнение полусферы принимает вид 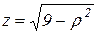 , а уравнение параболоида
, а уравнение параболоида 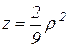 . Тогда
. Тогда
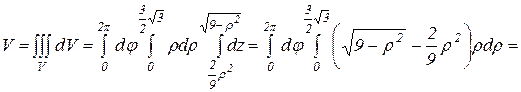
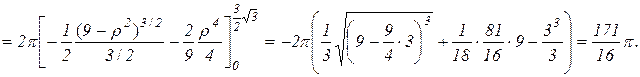
Ответ: V= 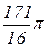 (ед.3).
(ед.3).
g
Пример 7 . Найти объем тела, ограниченного поверхностями 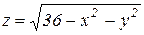 ,
, 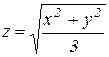 . Сделать чертеж тела и его проекции в плоскость
. Сделать чертеж тела и его проекции в плоскость 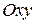 .
.
Решение:
| |||
 | |||

|


|
|

|

|
|
| |
|
Рис. 11.
Тело ограничено снизу поверхностью конуса 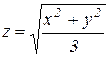 , а сверху - поверхностью полусферы
, а сверху - поверхностью полусферы 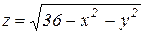 . Проекцией тела в плоскость
. Проекцией тела в плоскость 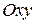 является круг с центром в начале координат. Уравнение ограничивающей его окружности получим после исключения из уравнений конуса и полусферы:
является круг с центром в начале координат. Уравнение ограничивающей его окружности получим после исключения из уравнений конуса и полусферы: 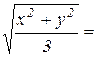
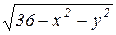 , или после простых преобразований:
, или после простых преобразований: 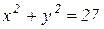 .
.
Объем тела  удобно вычислять, переходя к сферическим координатам. Запишем в сферических координатах (9) уравнение сферы и конуса:
удобно вычислять, переходя к сферическим координатам. Запишем в сферических координатах (9) уравнение сферы и конуса: 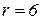 и
и 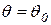 , где
, где 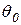 - угол при вершине конуса, который найдем из уравнения
- угол при вершине конуса, который найдем из уравнения 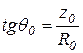 (см. рис. 11). Мы нашли, что
(см. рис. 11). Мы нашли, что 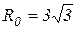 , тогда
, тогда 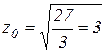 (из уравнения конуса). Следовательно,
(из уравнения конуса). Следовательно, 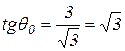 и
и 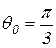 . Уравнение конуса в сферических координатах:
. Уравнение конуса в сферических координатах: 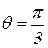 .
.
Тогда объем тела по формуле (14) равен
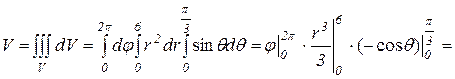


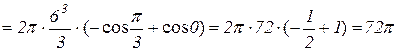 .
.
Ответ: V= 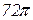 (ед.3).
(ед.3).
g
Пример 8 . Найти массу тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1, если задана его плотность γ(x, y, z)= 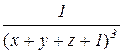 Сделать чертеж данного тела и его проекции в плоскость Oxy.
Сделать чертеж данного тела и его проекции в плоскость Oxy.
Решение: Заданное тело ограничено координатными плоскостями и наклонной плоскостью (см. рис. 12)
Массу тела вычислим по формуле (15):
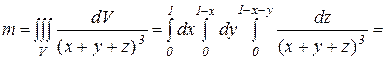
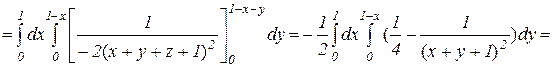
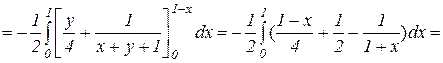
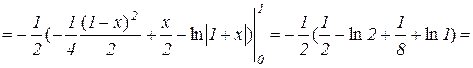
 0,034.
0,034.
| |
| |
| |
| |
|
|
|

|
|
| |
| |
|
|
|
| |
|



x+y=1
Рис.12
Ответ: m  0,034 (ед. массы).
0,034 (ед. массы).
g
Пример 9. Найти массу тела с плотностью γ(x, y, z)=x2+y2, ограниченного поверхностями z= 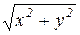 , z=2-x2-y2 . Сделать чертеж тела и его проекции в плоскость Oxy.
, z=2-x2-y2 . Сделать чертеж тела и его проекции в плоскость Oxy.
Решение: Заданное тело ограничено поверхностями конуса z= 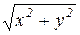 и параболоида z=2-x2-y2. Проекцией тела в плоскость Oxy является круг, ограниченный окружностью x2+y2=1 (см. рис. 13).
и параболоида z=2-x2-y2. Проекцией тела в плоскость Oxy является круг, ограниченный окружностью x2+y2=1 (см. рис. 13).


|

| |
|




|

|


|

| |
| |
| |
Рис. 13
Ограничивающие тело поверхности имеют простые уравнения в цилиндрической системе координат (8): конус z=ρ, параболоид z=2-ρ2. Массу тела вычислим по формуле (15); записав функцию плотности в цилиндрических координатах: γ=ρ2. Тогда
m= 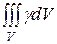 =
= 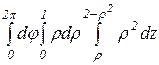 =
=
= 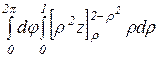 =
= 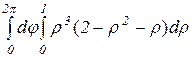 =
=
= 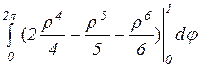 =2
=2 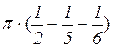 =
= 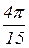
Ответ: m= 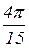 (ед. массы).
(ед. массы).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисление
для ВТУЗов. Том 2. - М.: Наука, 1978. - 430 с.
2. Задачи и упражнения по математическому анализу для ВТУЗов
/Под ред. Б.П.Демидовича. - М.: Наука, 1977. - 472 с.
Разработали: В.В.Аверин, канд. техн. наук, доцент
М.Ю.Соколова, канд. техн. наук, доцент
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|