Хелпикс

Главная

Контакты

Случайная статья



Оформление сводной таблицы результатов

⇐ ПредыдущаяСтр 4 из 4


Оформление сводной таблицы результатов

 

Сводная таблица результатов по исследованию

статических и динамических свойств объекта управления

Канал

Статика

Динамика

Средние результаты
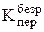
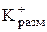
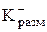
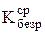
Т, мин.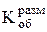
вх®вых                  

 

Приложение 4.

Оформление структурной схемы объекта

 

Структурная схема объекта

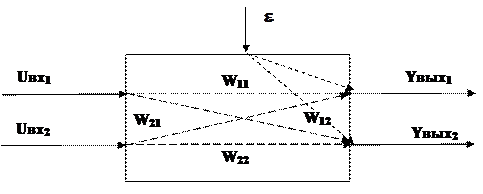
где Uвх1, Uвх2 – входные регулирующие (управляющие) переменные; Yвых1, Yвых2 – выходные регулируемые (управляемые) параметры; e - вектор возмущений; Wij – передаточные функции по каналам регулирования, перекрестным связям, по каналам возмущений.


Приложение 5.

Тема: Построение и анализ статических и динамических характеристик объектов управления.

 

    Работа большинства объектов регулирования заключается в преобразовании по определенному закону материальных и энергетических потоков. При этом возможны два принципиально различных режима работы: статический и динамический.

    В статическом (установившемся) режиме объект находится в равновесии, приток вещества или энергии равен стоку. Признаком статического режима работы является сохранение постоянного во времени значения выходного сигнала объекта (Хвых(t)=const). В статическом режиме каждому значению сигнала на входе соответствует определенное значение выходного сигнала:

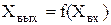.                                     (1)

Зависимость (1), которая связывает значения выходного и входного параметров объекта в установившемся режиме, называется статической характеристикой. Статическая характеристика может быть линейной и нелинейной.

В реальных условиях эксплуатации, когда на объект регулирования воздействуют различные возмущения, динамический режим работы объектов является характерным режимом. Поэтому определение динамической характеристики, составляет главную задачу при анализе САР.

Динамическая характеристика – кривая изменения выходного параметра во времени при изменении входной переменной.

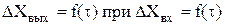                         (2)

При ступенчатом входном воздействии динамическая характеристика называется кривой отклика.

Существует два метода определения статических и динамических характеристик: аналитический и экспериментальный.

При использовании аналитического метода определения характеристик за основу берут уравнения математической модели объекта. Если необходимо определить статическую характеристику, то уравнения для статического режима работы, если необходимо определить динамическую характеристику – уравнения для динамического режима работы объекта.

Для построения статической характеристики необходимо рассчитать не менее пяти точек, причем центральной будет являться "рабочая" точка, соответствующая установившемуся режиму при заданных исходных данных.

Рис. 2. Статические характеристики объектов:

а) линейная; б) нелинейная

По статической характеристике определяют значение коэффициента передачи по данному каналу. Коэффициент передачи или коэффициент усиления выражает отношение изменения выходной переменной к изменению входной переменной и является размерной величиной:

.

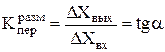Для объективного сравнения коэффициентов передачи по различным каналам удобнее оперировать безразмерными величинами. Для этого необходимо домножить числитель и знаменатель на соответствующие значения величин в "рабочей" точке. Например:

если , тогда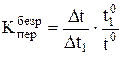

Динамическая характеристика строится при изменении входной переменной от " рабочей" точки в положительном и отрицательном направлении, другими словами при положительной и отрицательной ступеньке. При линейной статической характеристике по данному каналу, динамическая характеристика при ±Dвх. получается симметричной; при нелинейной – несимметричной.

Рис. 3. Динамические характеристики объектов при ±DХвх:

а) симметричная; б) несимметричная

Анализ динамической характеристики позволяет сделать вывод о том, какому динамическому звену соответствует кривая отклика (пропорциональное, интегральное, апериодическое, комбинация звеньев и т.д.); позволяет определить основные параметры данного звена, например, коэффициент передачи, постоянную времени (см. рис.3).

; ; ; ;

.

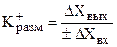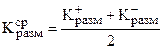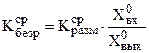Таким образом, по данным полученным по статическим и динамическим характеристикам объекта по различным каналам, мы можем представить математическую модель объекта в виде системы передаточных функций, а по величине безразмерных коэффициентов передачи, рекомендовать регулирующие переменные по каналам управления.


⇐ Предыдущая1234
  

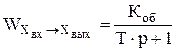
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.