ЛАБОРАТОРНАЯ РАБОТА. Параллельное соединение индуктивности и емкости при синусоидальных напряжениях и токах.. ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ. КРАТКАЯ ХАРАКТЕРИСТИКА ОБЪЕКТА ИССЛЕДОВАНИЯ

ЛАБОРАТОРНАЯ РАБОТА

Параллельное соединение индуктивности и емкости при синусоидальных напряжениях и токах.

1. ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ

Экспериментально исследовать работу электрической цепи однофазного синусоидального тока с параллельным соединением элементов:

1. исследование влияния величины индуктивности катушки на электрические параметры цепи однофазного синусоидального напряжения с параллельным соединением элементов;

2. опытное определение условий возникновения в данной цепи резонанса токов;

3. построить векторные диаграммы и резонансные кривые при последовательном соединении катушки и конденсатора;

4. научиться вычислять параметры цепи и строить векторные диаграммы цепи с параллельным соединением элементов.

2. КРАТКАЯ ХАРАКТЕРИСТИКА ОБЪЕКТА ИССЛЕДОВАНИЯ

1. ПАРАЛЛЕЛЬНАЯ ЦЕПЬ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА

На рис. 4.1 представлена электрическая цепь однофазного синусоидального напряжения с параллельным соединением двух приемников, один их которых на схеме замещен последовательным соединением резистора и емкостного элемента, а второй - последовательным соединением резистора и индуктивного элемента.

Токи в приемниках определяются по закону Ома

i=IL I ₌и ¹ V ²

где U - действующее значение напряжения источника электрической энергии;

I_], I₂ - токи в параллельных ветвях цепи;

Zj, Z₂ - полные сопротивления ветвей.

Z_l=^+X²_c,Z₂=^+Xl, (4.2)

где R_]2 X_C - активное и емкостное сопротивление первой ветви;

R₂, X_L - активное и индуктивное сопротивление второй ветви.

Вектор тока источника электрической энергии равен сумме векторов токов приемников

^/=/i^+/2. (4.3)

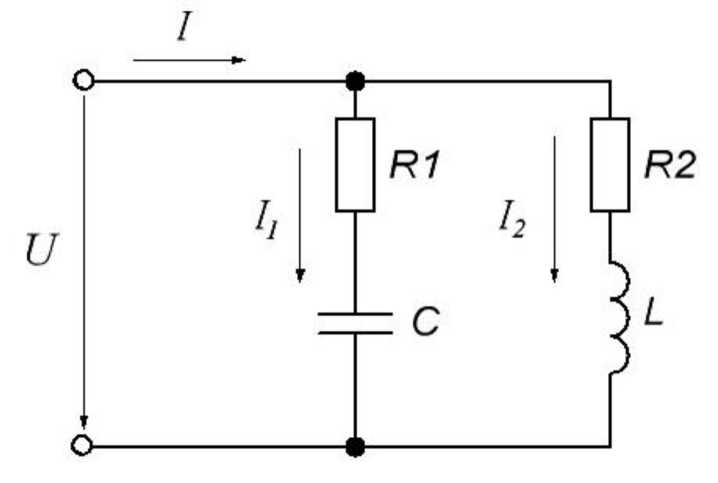
Рис. 4.1. Параллельная цепь переменного тока

При исследовании процессов в цепях с параллельным соединением приемников вектор тока в каждой ветви условно представляют в виде суммы векторов активной и реактивной составляющих тока. Вектор активной составляющей тока I_a совпадает по направлению с вектором напряжения U, а вектор реактивной составляющей I_pперпендикулярен этому вектору (рис. 4.2).

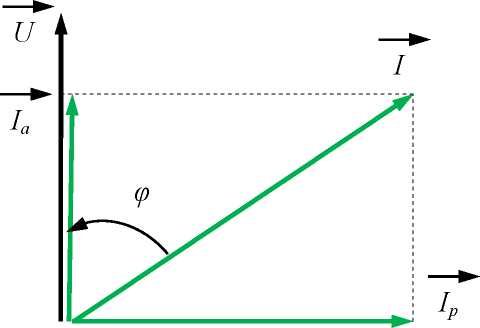
Рис. 4.2. Разложение тока на активную и реактивную составляющие

Из треугольника токов (рис. 4.2) величины активной и реактивной составляющих тока определяются

I_a ⁼ I cos (р; I_p=Ism

(4.4)

где ф - угол сдвига фаз между напряжением и током.

На рис. 4.3 представлена векторная диаграмма напряжений и токов для параллельной цепи переменного тока, приведенной на рис. 4.1.

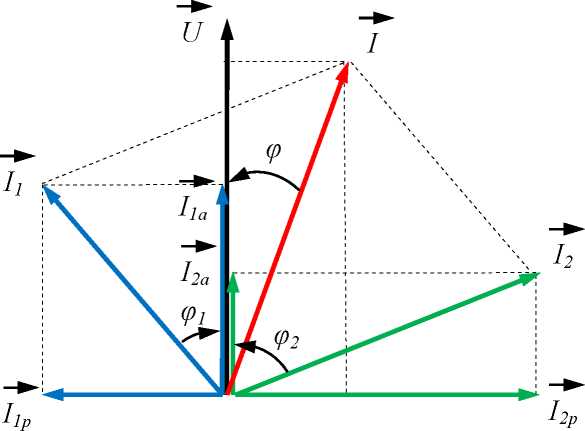
Рис. 4.3. Векторная диаграмма напряжений и токов параллельной цепи переменного тока

Величины активной и реактивной составляющих токов приемника

ha = Acoscpi; I_lp =/₁sincp₁; (4.5)

I_2a=I₂ coscp₂; h_P=^J₂ sincp₂, (4.6)

где ф\ и ф₂ - углы сдвига фаз между вектором напряжения U и векторами токов I\ и I₂.

Представление токов активными и реактивными составляющими позволяет путем их сложения найти активную I_a и реактивную I_p составляющую тока источника и по ним определить ток источника I

Иногда при расчетах параллельных цепей переменного тока используют понятия проводимости. Активная, реактивная и по лная про во димости связаны с активными и реактивными сопротивлениями этих же ветвей равенствами

= —• h = — - Y = - ^g Z² ’ Z² ’ Z'

Полная проводимость всей ветви определяется выражением

Y = Jg² +b²=Jg² + (b_L -b_c)² , (4.11)

N N N

где g = ^g_r, b_L = ^b_LK, b_c = ^b_CK - активная, индуктивная и ем-

К=1 К=1 К=1

костная проводимости всей электрической цепи, равные сумме всех активных, индуктивных и емкостных проводимостей отдельных параллельных ветвей;

b_L - b_C = b - реактивная проводимость всей электрической цепи.

Угол сдвига фаз между общим током цепи и напряжением источника питания

Ъ -Ъ

(p = arctg— (4.12)

g

Активные и реактивные проводимости связаны с полной проводимостью выражениями

g = Zcos^; b = Y-sin^. (4.13)

Величина общего тока, потребляемого участком цепи с параллельным соединением активных, индуктивных и емкостных сопротивлений, определяется выражением

I = UY, (4.14)

где U - напряжение на зажимах цепи;

Y - полная проводимость всей цепи.

1.

2. РЕЗОНАНС ТОКОВ

В электрических цепях с параллельным соединением приемников, содержащих индуктивные и емкостные элементы, может, при определенных условиях, возникать явление резонанса токов. Резонансом токов называется режим, при котором ток источника электрической энергии совпадает по фазе с напряжением источника, т.е. ф = 0.

Применительно к электрической цепи, изображенной на рис. 4.1:

Q = Ql~Qc =Ssincp = 0; I_p =I_2p-I_lp =/sin(p = 0. (4.15)

Следовательно, условием резонанса токов является равенство нулю реактивной мощности цепи и реактивной составляющей тока источника электрической энергии.

Из условия резонанса токов следует, что

Ql = Qc, ^I1p = ^I2p. ⁽⁴¹⁶⁾

При резонансе токов коэффициент мощности цепи

Р I , coscp = — = — = 1.

SI

Ток в ветви с источником электрической энергии содержит только активную составляющую, является минимальным по величине и может оказаться значительно меньше токов в каждом из параллельно включенных приемников

¹ = ^I1a + ha = h = ¹min. ⁽⁴¹⁸⁾

1.

3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ИДЕАЛЬНОЙ ЕМКОСТИ И РЕАЛЬНОЙ КАТУШКИ ИНДУКТИВНОСТИ

Рассмотрим электрическую цепь параллельно соединенных идеальной емкости и реальной катушки индуктивности. В большинстве случаев такие допущения делаются на практике (рис. 4.4).

Рассмотрим три возможных случая.

1. При Ъь > be нагрузка имеет индуктивный характер. Вектор общего тока I отстает по фазе от вектора напряжения Uна угол ф (рис. 4.5).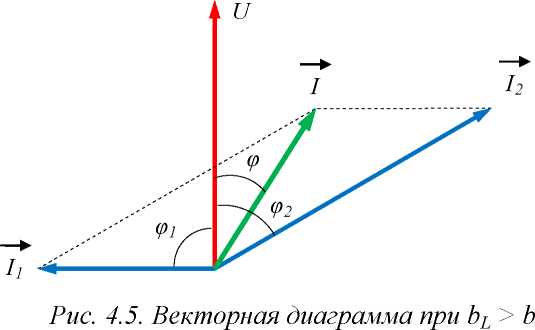

Ток через конденсатор I₁ = b_CU. Ток через индуктивность I₂ = b_LU. При этом ток через конденсатор по величине меньше тока через катушку индуктивности

I < 1₂. (4.19)

2. При bL < bC цепь имеет емкостной характер. Вектор общего тока I опережает по фазе вектор напряжения U источника на угол ф (рис. 4.3).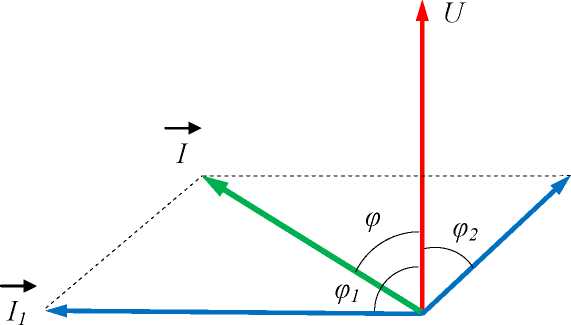

Ток через конденсатор по величине больше тока через катушку индуктивности

Ii > h. (4.20)

3. Если b_L = b_C, в цепи наступает резонанс токов, при котором сдвиг фаз между общим напряжением и общим током оказывается равным нулю (рис. 4.7).

Общее сопротивление цепи при резонансе резко увеличивается, а общий ток I уменьшается и становится минимальным

I = U-Y = Uyjg² + b_L-b_c ² =U-g. (4.21)

Таким образом, полное сопротивление цепи оказывается чисто активным и очень высоким (g - малая величина, определяемая омическим сопротивлением проводов катушки: Y = g).

Энергетический процесс при резонансе можно рассматривать как наложение двух процессов: необратимого преобразования потребляемой от источника энергии в тепло, выделяемое в активном сопротивлении, и процесса, представляющего собой колебание энергии внутри цепи - между магнитным полем катушки индуктивности и электрическим полем конденсатора. Первый процесс характеризуется величиной активной мощности Р, а второй - величиной реактивной мощности Ql = Qc. Колебания между источником и цепью не происходит: ^Q = ^ql ^{- Q}c = 0.

Если активная проводимость катушки меньше ее индуктивной проводимости, то токи через катушку и конденсатор могут значительно превышать общий ток I. Превышение токов 11 и I₂ над общим током характеризует параметр цепи, который называется коэффициентом добротности

Резонансные явления очень широко применяются в электротехнике и в радиотехнических устройствах. Электрические фильтры различных электротехнических устройств являются также резонансными цепями.

12 3 Следующая ⇒