
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Уравнение касательной к графику функции.
Тема: Уравнение касательной к графику функции.
“Человек лишь там чего–то добивается, где он верит в свои силы”
Л. Фейербах
Ход урока.
Вспомним, что же такое касательная?
“Касательная – это прямая, имеющая с данной кривой одну общую точку”.
Обсуждение правильности данного определения. (После обсуждения, учащиеся приходят к выводу, что данное определение неверно.) Для наглядного доказательства их умозаключения приводим следующий пример.
Рассмотрим пример.
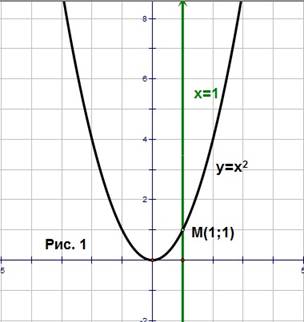
Пусть дана парабола 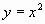 и две прямые
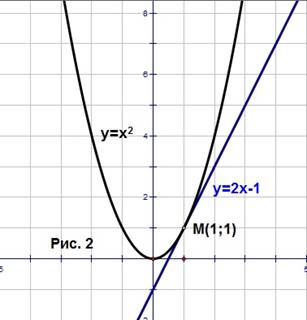
и две прямые 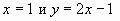 , имеющая с данной параболой одну общую точку М (1;1). Проводится обсуждение, почему первая прямая не является к данной параболе касательной, а вторая является.
, имеющая с данной параболой одну общую точку М (1;1). Проводится обсуждение, почему первая прямая не является к данной параболе касательной, а вторая является.
 |  | ||
На данном уроке, мы с вами должны выяснить, что же такое касательная к графику функции в точке, как составить уравнение касательной?
Рассмотреть основные задачи на составление уравнения касательной.
Для этого, вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной и правила дифференцирования.
Изучение нового материала.
Чтобы задать уравнение прямой на плоскости нам достаточно знать угловой коэффициент и координаты одной точки.
Пусть дан график функции 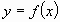 . На нем выбрана точка
. На нем выбрана точка 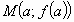 , в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
, в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
Дадим аргументу приращение 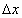 и рассмотрим на графике (Рис. 3) точку P с абсциссой
и рассмотрим на графике (Рис. 3) точку P с абсциссой 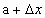 . Угловой коэффициент секущей MP, т.е. тангенс угла между секущей и осью x, вычисляется по формуле
. Угловой коэффициент секущей MP, т.е. тангенс угла между секущей и осью x, вычисляется по формуле 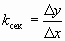 .
.
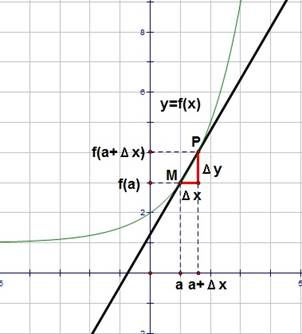
Если мы теперь устремим 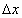 к нулю, то точка Р начнет приближаться по кривой к точке М. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной
к нулю, то точка Р начнет приближаться по кривой к точке М. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной 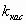 будет вычисляться по формуле
будет вычисляться по формуле 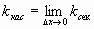 .
.
Следовательно, 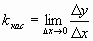 .
.
Если к графику функции y = f (x) в точке х = а можно провести касательную, непараллельную оси у, то выражает угловой коэффициент касательной.
Или по другому. Производная в точке х = а равна угловому коэффициенту касательной к графику функции y = f(x)в этой точке 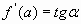 .
.
Это и есть геометрический смысл производной.
Причем, если :
1. 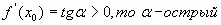
2. 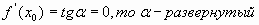
3. 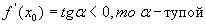 .
.
Выясним общий вид уравнения касательной.
Пусть прямая задана уравнением 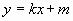 . Мы знаем, что
. Мы знаем, что 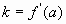 . Для вычисления m воспользуемся тем, что прямая проходит через точку
. Для вычисления m воспользуемся тем, что прямая проходит через точку 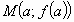 . Подставим в уравнение. Получим
. Подставим в уравнение. Получим 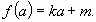 , т.е.
, т.е. 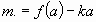 . Подставим найденные значения k и m в уравнение прямой:
. Подставим найденные значения k и m в уравнение прямой:
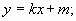
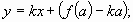
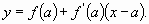 – уравнение касательной к графику функции.
– уравнение касательной к графику функции.
Рассмотрим примеры:
Составим уравнение касательной:
1. к параболе 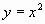 в точке
в точке 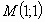
2. к графику функции 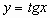 в точке
в точке 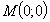
Решая эти примеры, мы воспользовались очень простым алгоритмом, который заключается в следующем:
1. Обозначим абсциссу точки касания буквой a.
2. Вычислим 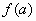 .
.
3. Найдем 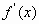 и
и 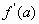 .
.
4. Подставим найденные числа 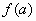 ,
, 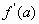 в формулу
в формулу 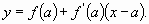
Рассмотрим типичные задания и их решение.
№1.Составить уравнение касательной к графику функции 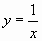 в точке
в точке 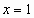 .
.
Решение.Воспользуемся алгоритмом, учитывая, что в данном примере 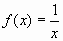 .
.
1) 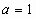
2) 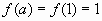
3) 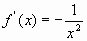 ;
; 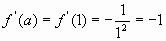
4) Подставим найденные числа 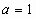 ,
, 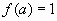 ,
, 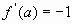 в формулу.
в формулу.
Получим:
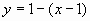 , т.е.
, т.е. 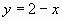
Ответ: 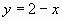
№2. К графику функции 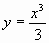 провести касательную так, чтобы она была параллельна прямой
провести касательную так, чтобы она была параллельна прямой 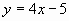 .
.
Решение.Уточним формулировку задачи. Требование “провести касательную” обычно означает “составить уравнение касательной”. Воспользуемся алгоритмом составления касательной, учитывая, что в данном примере 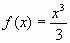 .
.
Искомая касательная должна быть параллельна прямой 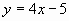 . Две прямые параллельны, тогда и только тогда, когда равны их угловые коэффициенты.Значит угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой:
. Две прямые параллельны, тогда и только тогда, когда равны их угловые коэффициенты.Значит угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: 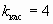 .Но
.Но 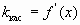 . Следовательно:
. Следовательно: 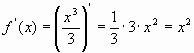 ;
; 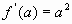 .
.
Из уравнения 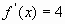 ,т.е.
,т.е. 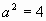 , находим, что
, находим, что 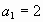 и
и 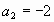 . Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Действуем по алгоритму.
1) 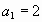 ,
, 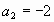
2) 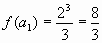 ,
, 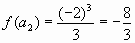
3) 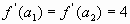
4) Подставив значения 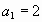 ,
, 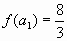 ,
, 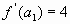 , получим
, получим 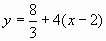 , т.е.
, т.е. 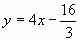 .
.
Подставив значения 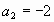 ,
, 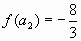 ,
, 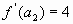 , получим
, получим 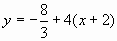 , т.е.
, т.е. 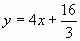
Ответ: , .
V. Решение задач.
1. Решение задач на готовых чертежах
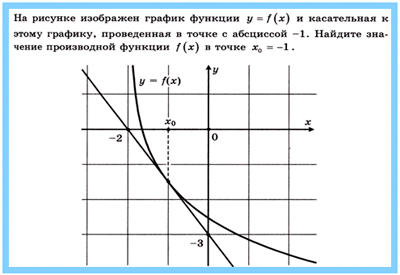
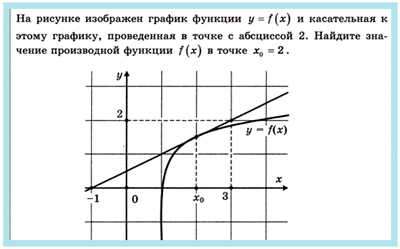
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|