Хелпикс

Главная

Контакты

Случайная статья



Ход урока. Изучение нового материала.



 

Тема: "Угол между прямыми"

Ход урока

1. Основание призмы ABCDA1B1C1D1 – трапеция. Какие из следующих пар прямых являются скрещивающими?

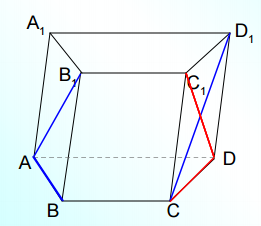
Ответ: ABи CC1,A1D1и CC1.

Изучение нового материала.

Расположение прямых в пространстве и угол между ними.

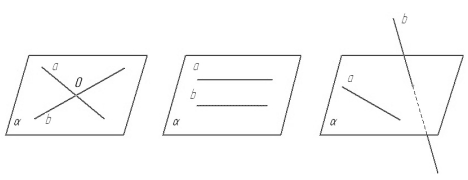
1. Пересекающиеся прямые.

2. Параллельные прямые.

3. Скрещивающиеся прямые.

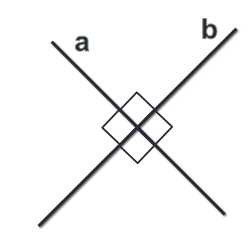
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

 

 
α
a
b

 


Слайд 6

Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.

 

Угол между двумя параллельными прямыми равен 0°.

 

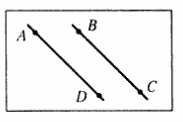
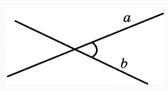Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.

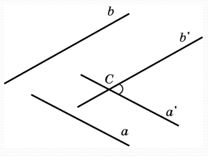
Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямым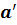и и .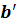

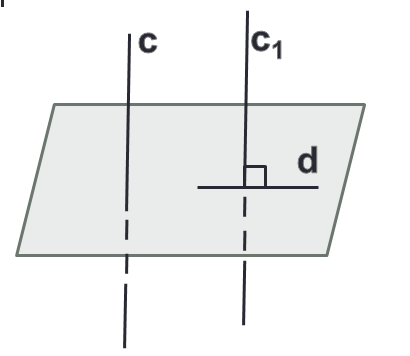
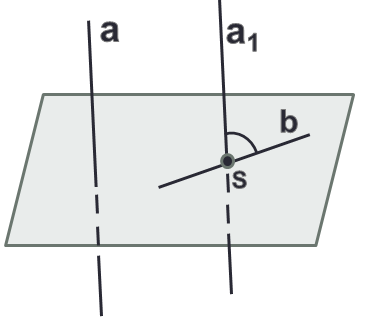Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными.

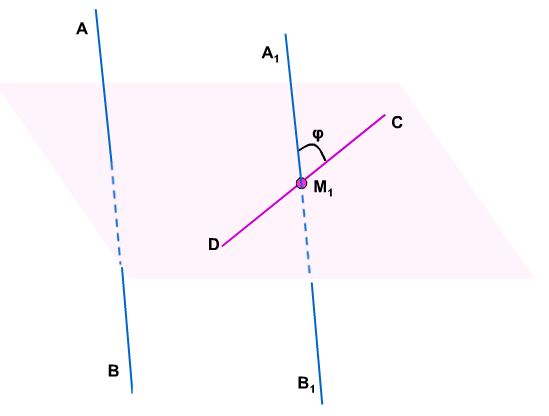
Угол между скрещивающими прямыми.

Пусть ABи CD – две скрещивающиеся прямые.

Возьмём произвольную точку М1 пространства и проведём через неё прямые А1В1 и C1D1, соответственно параллельные прямым AB и CD.

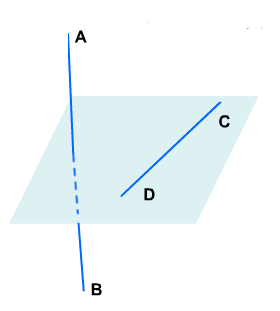
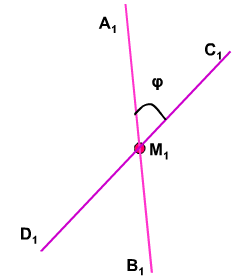
Если угол между прямыми А1В1 и C1D1равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.

Найдём угол между скрещивающимися прямыми ABи CD.

В качестве точки M1можно взять любую точку на одной из скрещивающихся прямых.

2. Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.

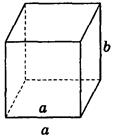а) 90°;  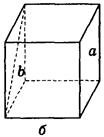                          б) 45°;

Слайд 16

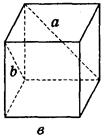в) 60°;  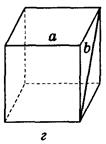                           г) 90°;

Слайд 17

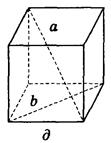д) 90°;  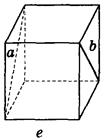                          е) 90°.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.