I. Вычисление углов между прямыми, прямой и плоскостью

I. Вычисление углов между прямыми, прямой и плоскостью

№1.

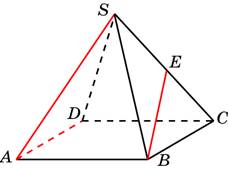В правильной пирамиде SABCD, все ребра которой равны 1, точка E– середина ребра SC.Найдите угол между прямыми ADи BE.

Решение:

Искомый угол = углу CBE.Треугольник SBC-равносторонний.

ВE – биссектриса угла = 60. Угол CBE равен 30.

Ответ:30°.

№2.

Какой угол называется углом между скрещивающими прямыми?

Ответ:

Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a₁и b₁, причем a₁|| a, b₁ || b.

№3.

Угол между прямымиaи bравен 90°. Верно ли, что прямые aи bпересекаются?

Ответ:

Неверно, так как прямые могут либо пересекаться, либо скрещиваться.

№4.

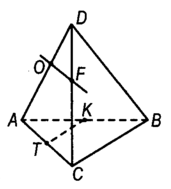DABC – тетраэдр, точка О и F – середины ребра AD и CDсоответственно, отрезок TK – средняя линия треугольника ABC.

a) Чему равен угол между прямымиOFи CB?

b) Верно ли, что угол между прямымиOFи TK равен 60°?

c) Чему равен угол между прямымиTFи DB?

Решение:

Дано: DABC,

О – середина AD,

F – серединаCD,

ТК – средняя линия ∆АВС.

Решение:

a) В плоскости АВС через точку С проходит прямая АС, параллельная прямой OF(т.к. OF – средняя линия ∆АВС, поэтому АСВ – угол между скрещивающимися прямыми OFт СВ. ∆АВС – правильный, поэтому АСВ=60°.
Ответ: 60°

b) Т.к. OF || AC и TK || CB, то угол между прямымиOF и TK равен углу между прямыми AC и CB, т.е. 60°.
Ответ: верно.

c) Т.к. TF || AD (по свойству средней линии), то 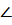ADB=60°.
Ответ: 60°