Хелпикс

Главная

Контакты

Случайная статья



УРОК АЛГЕБРЫ ОТ 22.04.2020

Стр 1 из 2Следующая ⇒


УРОК АЛГЕБРЫ ОТ 22.04.2020

 Решение простейших тригонометрических уравнений (теория+примеры)

 

Все тригонометрические уравнения сводятся к простейшим. Поэтому особое внимание следует уделять решению простейших уравнений. Начинать нужно с самых простых.

К простейшим тригонометрическим уравнениям относятся уравнения вида:

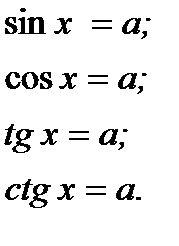
Для каждого из простейших тригонометрических уравнений определены формулы, справедливость которых обосновывается с помощью тригонометрического круга и с учетом периодичности тригонометрических функций.

 

Sin x=а, |а|>1, решений нет;           sin x=0,  x= πn, nєZ   sin x =–1, x= – +2πn, nєZ;   sin x =1, x= +2πn, nєZ;   sin x=а, |а|<1,  x= arcsin а +2πn, nєZ;                               x= π–arcsin а +2πn, nєZ. В последнем случае для сокращения записи используют формулу: x=(–1)narcsinа + πn, nєZ. (основная формула)                             cos x=а, |а|>1,решений нет;   cos x=0, x= – +πn, nєZ;   cos x=–1, x= π +2πn, nєZ;   cos x=1, x=2πn, nєZ;   cos x=а, |а|<1,    x= ± arccosа +2πn, nєZ. (основная формула)                            

 

Решения уравнения tg x=а и ctg x=а записываются существенно проще:

 x= arctgа +πn, nєZ и, соответственно, x= arcсtgа +πn, nєZ .                           

Пример 1. Решить уравнение sinx = .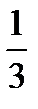

Решение: так как 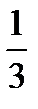<1, значит x=(–1)narcsin  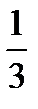+ πn, nєZ.  

Ответ: (–1)narcsin 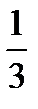 + πn, nєZ.                       

Пример 2. Решить уравнение cos x = .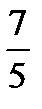

Решение: так как 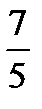 >1, значит,  уравнение не имеет решения.

Ответ: нет решения.

Пример 3. Решить уравнение tg x+ 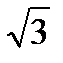 = 0.

Решение: 

tg x+ 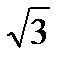 = 0                        

tg x = –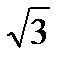

x = arctg (– 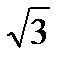) + πn, nєZ

x = – arctg 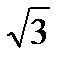+ πn, nєZ

x = – 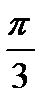+2πn, nєZ;

Ответ: – 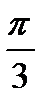+2πn, nєZ.

Пример 4. Решить уравнение 2cos x = – .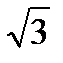 

Решение:

2cos x = –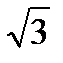  

cos x = –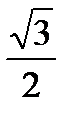                                     

x= ± arccos (– 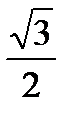)+2πn, nєZ

x= ±( π – arccos 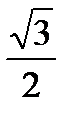)+2πn, nєZ        

x= ±( π – 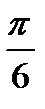)+2πn, nєZ

x = ± 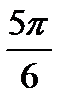  + 2πn, nєZ

Ответ: ± 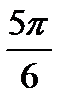  + 2πn, nєZ.

Далее нужно переходить к решению более сложных уравнений, которые чаще всего встречаются в вариантах ЕГЭ в разделе А.

Пример 5. Решить уравнение cos  = .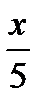                             

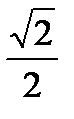Решение: cos  =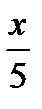

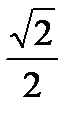
Это уравнение сводится к простейшему cos t = 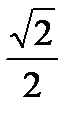 заменой t = 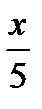, которую можно не     прописывать.

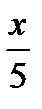 = ± arccos 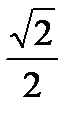+2πn, nєZ           

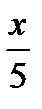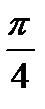 = ± +2πn, nєZ

 х = ± 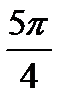+ 10πn, nєZ

Ответ: ± 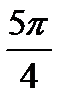 + 10πn, nєZ.

 

Домашнее задание:

1. Изучить теорию по теме «Решение простейших тригонометрических уравнений»;

2.  По образцу примеров №1-5 решить №3(а, к), 4(а, г) на с.299

3. Д/з прислать к 24.04. до 15.00

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.