
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Линия тангенсов.. Уравнение tg x = a
Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная АВ к единичной окружности, параллельная оси ординат (см. рисунок).
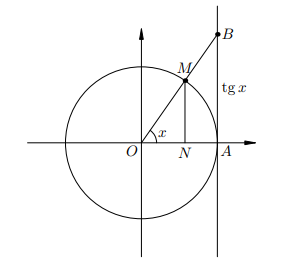
Из подобия треугольников ОАВ и ONM имеем:
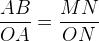
Но OA=1, MN=sin x, ON=cos x, поэтому AB=tg x
Мы рассмотрели случай, когда x находится в первой четверти. Аналогично рассматриваются случаи, когда x находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
 Тангенс угла x равен ординате точки B, которая является точкой пересечения линии тангенсов и прямой OM.
Тангенс угла x равен ординате точки B, которая является точкой пересечения линии тангенсов и прямой OM.
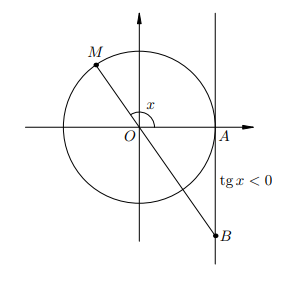
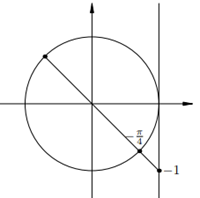
Вот рисунок в случае, когда x находится во второй четверти. Тангенс угла x отрицателен.
Уравнение tg x = a
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение tg x = a имеет решения при любом a.
tg x = 0
Имеем диаметральную горизонтальную пару точек:
Эта пара, как мы уже знаем, описывается формулой:
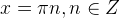
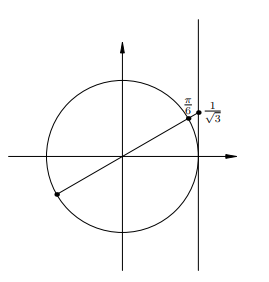
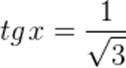
Имеем диаметральную пару:
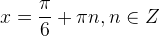
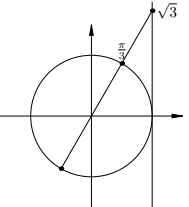
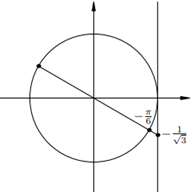
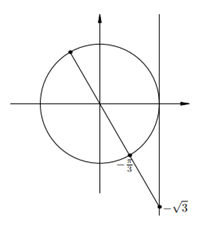
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
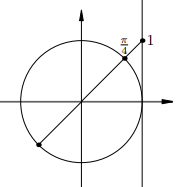 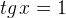 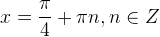
|  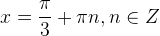 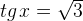
|  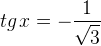
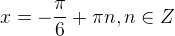
|
 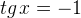
| 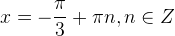 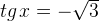 
|
.
Уравнение tg x = a имеет решения при любом a. Эти решения изображаются диаметральной парой точек:
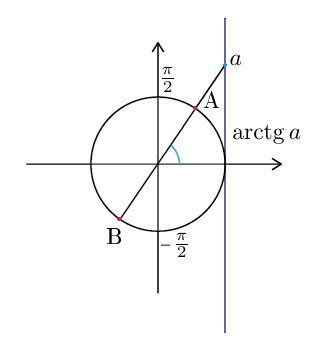 Как и в случае арксинуса, роль арктангенса отведена правой точке. Точнее:
Как и в случае арксинуса, роль арктангенса отведена правой точке. Точнее:
Арктангенсом числа 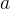 называется угол , такой, что
называется угол , такой, что 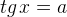 .
.
Обозначение: 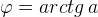 . Область определения арктангенса – промежуток
. Область определения арктангенса – промежуток 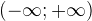 . Область значений –интервал (-П/2;П/2).
. Область значений –интервал (-П/2;П/2).
На нашем рисунке 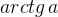 является одним из углов, соответствующих точке
является одним из углов, соответствующих точке 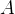 .
.
А почему в определении арктангенса исключены концы промежутка – точки 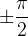 ? Дело в том, что тангенс в этих точках не определён. Не существует числа
? Дело в том, что тангенс в этих точках не определён. Не существует числа 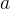 , равного тангенсу какого либо из этих углов.
, равного тангенсу какого либо из этих углов.
Записать решения уравнения tg x = a совсем просто 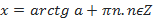
Тем самым мы фактически разобрались и с уравнением 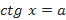 при
при 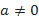 . В этом случае оно равносильно уравнению
. В этом случае оно равносильно уравнению 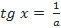 , и можно сразу записать ответ:
, и можно сразу записать ответ: 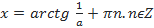
Но можно использовать и арккотангенс. Такая функция тоже существует, и вот её определение.
Арккотангенсом числа 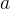 называется угол
называется угол 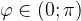 , такой, что ctg
, такой, что ctg 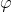 = a.
= a.
Тогда решения уравнения 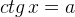 при любом
при любом 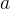 имеют вид:
имеют вид:
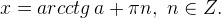
Подведём итог. Соберём формулы для решений простейших тригонометрических уравнений в небольшую таблицу.
| Уравнение | Решения |
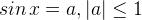
| 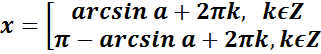
|
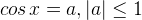
| 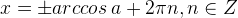
|
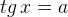
| 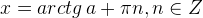
|
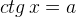
| 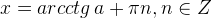
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|