
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Инструкция для обучающихся
Стр 1 из 2Следующая ⇒
| В1 В2 В3 | Вариант 1
Обязательная часть
При выполнении заданий выполните ход решения и запишите ответ. Ответом на задания В1-В12 должно быть целое число или конечная десятичная дробь.
Шоколадка стоит 31 рубль. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 170 рублей в воскресенье?
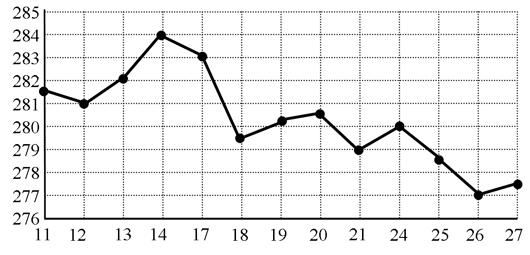
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 11 по 27 июля 2000 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену золота на момент закрытия торгов в указанный период (в долларах США за унцию).
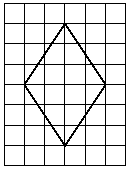
 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.
| В4 В5 В6 В7 В8 В9 В10 В11 | При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 8 тонн природного камня и 7 мешков цемента. Для бетонного фундамента необходимо 6 тонн щебня и 43 мешка цемента. Тонна камня стоит 1600 рублей, щебень стоит 750 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешёвый вариант?
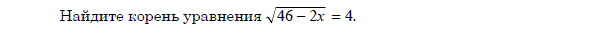 В треугольнике угол C=90º, cos A=
В треугольнике угол C=90º, cos A= 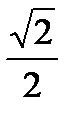 . Найдите tgA.
Найдите значение выражения: . Найдите tgA.
Найдите значение выражения:
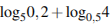 В правильной треугольной пирамиде SABC М -середина ребра ВС, S-вершина. Известно, что АВ=6, SM=19. Найдите площадь боковой поверхности пирамиды.
В правильной треугольной пирамиде SABC М -середина ребра ВС, S-вершина. Известно, что АВ=6, SM=19. Найдите площадь боковой поверхности пирамиды.
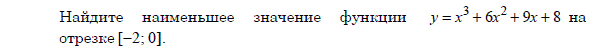 На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).
На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).
 Тоня, Арина, Маша, Денис, Лёня и Максим бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
Тоня, Арина, Маша, Денис, Лёня и Максим бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
|
| В12 С1 С2 С3 |  Дополнительная часть
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
Дополнительная часть
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
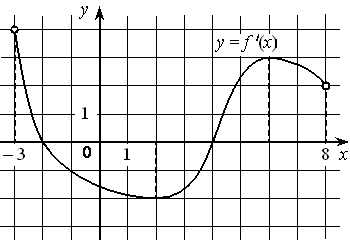
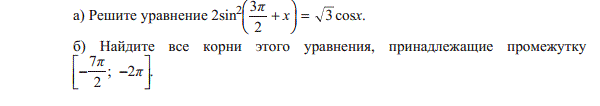 В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50.Найдите боковое ребро.
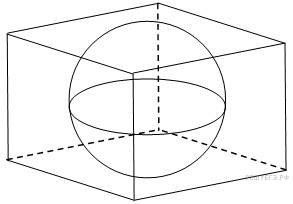
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50.Найдите боковое ребро.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
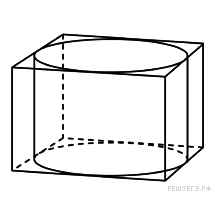
| С4 С5 С6 С7 | Решите систему уравнений.
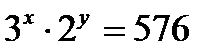
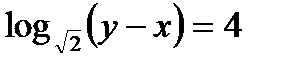 Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины С на расстоянии 14 и 48. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины С на расстоянии 14 и 48. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
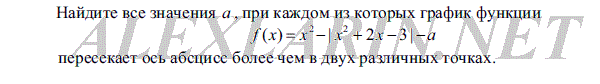 В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос про Александра Второго. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос про Александра Второго.
В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос про Александра Второго. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос про Александра Второго.
|
| В1 В2 В3 | Вариант 2
Обязательная часть
При выполнении заданий выполните ход решения и запишите ответ. Ответом на задания В1-В12 должно быть целое число или конечная десятичная дробь.
Билет на выставку стоит 200 рублей, а при групповом посещении действует скидка 20%. Сколько школьников сможет посетить выставку, если родительский комитет выделил на это 2300 рублей?
На рисунке жирными точками показано количество SMS, отправленных во время голосования на конкурсе "Евровидение" в период с 2004 по 2009 год. По горизонтали указываются года, по вертикали — количество SMS в тысячах штук. Для наглядности жирные точки на рисунке соединены линией.
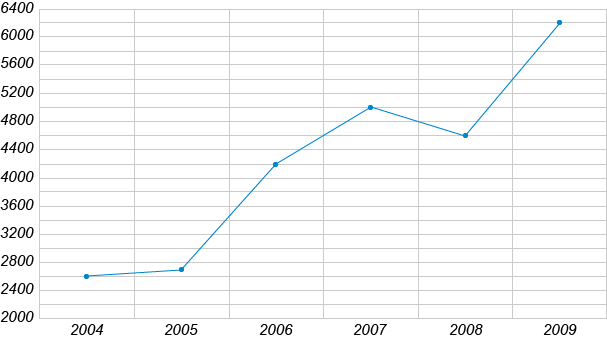 Определите по рисунку, на сколько тысяч увеличилось число SMS в 2009 году по сравнению с 2004 годом.
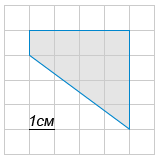
На клетчатой бумаге с клетками размером 1 см × 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Определите по рисунку, на сколько тысяч увеличилось число SMS в 2009 году по сравнению с 2004 годом.
На клетчатой бумаге с клетками размером 1 см × 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
| В4 В5 В6 В7 В8 В9 В10 В11 | Семья из трех человек едет из Москвы в г.Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 740 рублей. Автомобиль расходует 9 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19 руб. за литр. Сколько рублей будет стоить самая дешевая поездка для этой семьи?

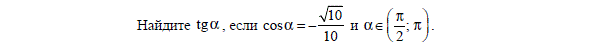
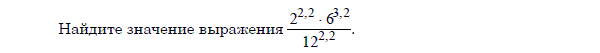 Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
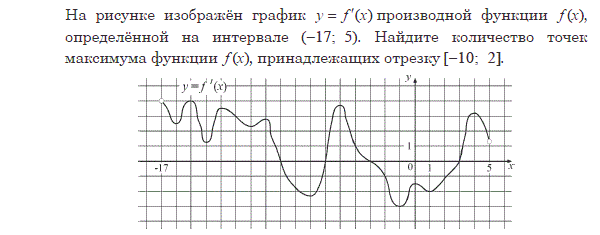
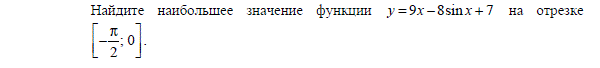 На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (−8;8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−4;6]
На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (−8;8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−4;6]
 Двое играют в кости – они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того , что он выиграет.
Двое играют в кости – они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того , что он выиграет.
|
| В12 С1 С2 С3 | 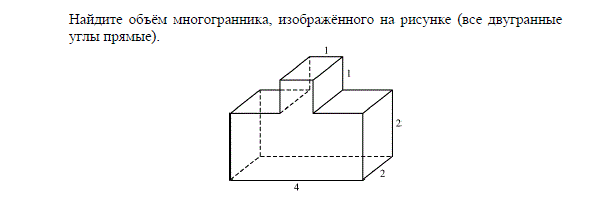 Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
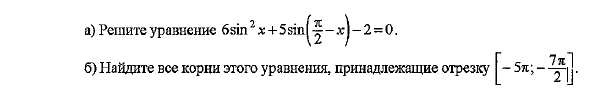 В правильной четырехугольной пирамиде высота равна 8. Площадь основания равна 18. Найдите боковое ребро.
В куб вписан шар радиуса 1. Найдите объем куба.
В правильной четырехугольной пирамиде высота равна 8. Площадь основания равна 18. Найдите боковое ребро.
В куб вписан шар радиуса 1. Найдите объем куба.
| С4 С5 С6 С7 | Решите систему уравнений.
lg x – lg y = 7
lg x + lg y = 5
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины С на расстоянии 14 и 48. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
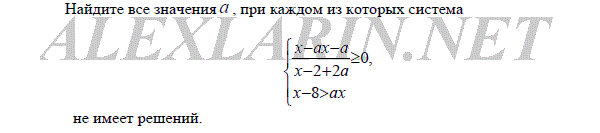 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
|
| В1 В2 В3 | Вариант 3
Обязательная часть
При выполнении заданий выполните ход решения и запишите ответ. Ответом на задания В1-В12 должно быть целое число или конечная десятичная дробь.
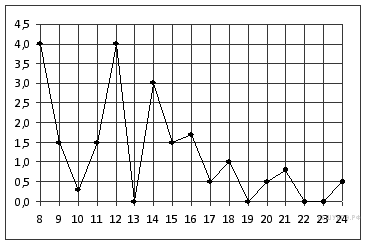
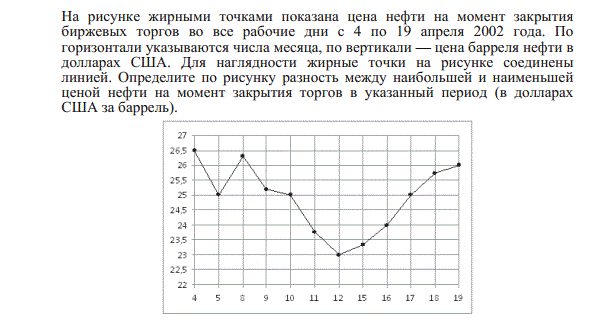
 На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах.
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах.
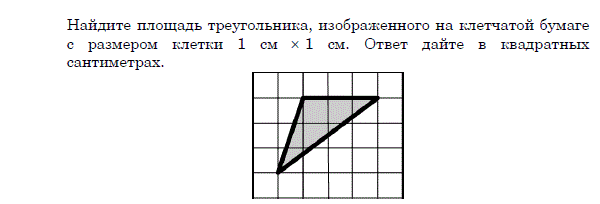
| В4 В5 В6 В7 В8 В9 В10 В11 |  Найдите корень уравнения
Найдите корень уравнения 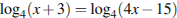
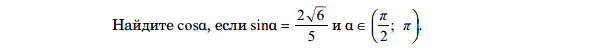
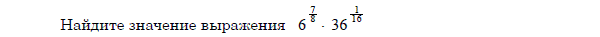 Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Найдите наибольшее значение функции y=9cosx+16x−8 на отрезке [−3π/2;0].
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Найдите наибольшее значение функции y=9cosx+16x−8 на отрезке [−3π/2;0].
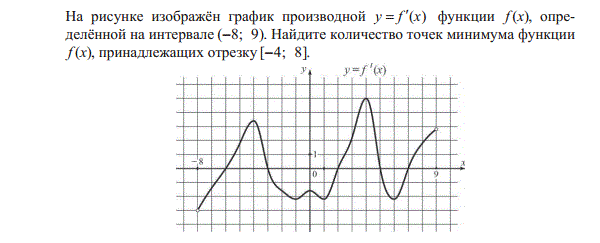

|
| В12 С1 С2 С3 | 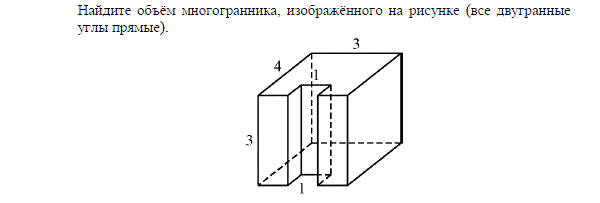 Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
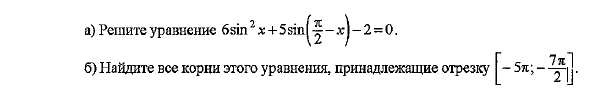 В правильной четырехугольной пирамиде высота равна 10. Площадь основания равна 72. Найдите боковое ребро.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
В правильной четырехугольной пирамиде высота равна 10. Площадь основания равна 72. Найдите боковое ребро.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
| С4 С5 С6 С7 | Решите систему уравнений.
4x·4y = 64
4x - 4y = 63
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины С на расстоянии 14 и 48. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
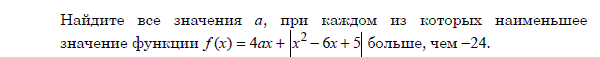 Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
.
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
.
|
| В1 В2 В3 | Вариант 4
Обязательная часть
При выполнении заданий выполните ход решения и запишите ответ. Ответом на задания В1-В12 должно быть целое число или конечная десятичная дробь.
Оля отправила SMS-cообщения с новогодними поздравлениями своим 17 друзьям. Стоимость одного SMS-сообщения 1 рубль 20 копеек. Перед отправкой сообщения на счету у Оли было 32 рубля. Сколько рублей останется у Оли после отправки всех сообщений?
 .
.

| В4 В5 В6 В7 В8 В9 В10 В11 |  Найдите корень уравнения
Найдите корень уравнения 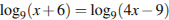
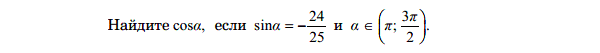
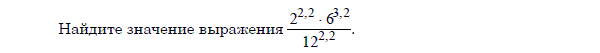 В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде 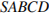 точка точка  — центр основания, — центр основания, 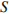 вершина, вершина,  , , 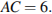 Найдите боковое ребро Найдите боковое ребро 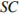 .
Найдите наименьшее значение функции y=6cosx−7x+8 на отрезке [−3π/2;0]. .
Найдите наименьшее значение функции y=6cosx−7x+8 на отрезке [−3π/2;0].

|
| В12 С1 С2 С3 | 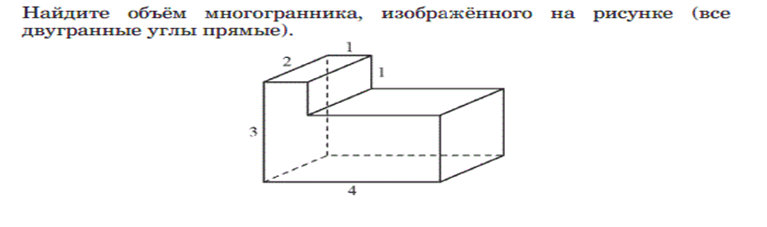 Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Часть 2
Для записи решения заданий С1-С7 запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
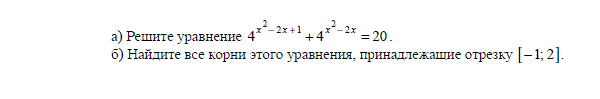 В правильной четырехугольной пирамиде высота равна 6. Площадь основания равна 25. Найдите боковое ребро.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
В правильной четырехугольной пирамиде высота равна 6. Площадь основания равна 25. Найдите боковое ребро.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
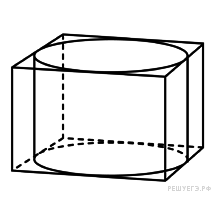
| С4 С5 С6 С7 | Решите систему уравнений.
√x - √y = 4
2√x + 3√y = 18
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины С на расстоянии 14 и 48. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
 Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
|
Инструкция для обучающихся
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|