
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уважаемый студент, добрый день.
Уважаемый студент, добрый день.
Конспект и решения с ответами прислать на e-mail: altjin46@rambler.ru или в личку ВК.
В тетрадь записываем число и свою фамилию собственноручно!
Напоминание не записывать
Геометрическая прогрессия — последовательность чисел {\displaystyle b_{1},b_{2},b_{3},\ldots }b1, b2, b3, … (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q{\displaystyle q}
(знаменатель прогрессии), где 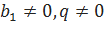 {\displaystyle b_{1}\neq 0}{\displaystyle q\neq 0}: {\displaystyle b_{1},b_{2}=b_{1}q,b_{3}=b_{2}q,\ldots ,b_{n}=b_{n-1}q}b1, b2=b1q, b3=b2q, …, bn=bn-1q, ….
{\displaystyle b_{1}\neq 0}{\displaystyle q\neq 0}: {\displaystyle b_{1},b_{2}=b_{1}q,b_{3}=b_{2}q,\ldots ,b_{n}=b_{n-1}q}b1, b2=b1q, b3=b2q, …, bn=bn-1q, ….
Любой член геометрической прогрессии может быть вычислен по формуле bn=b1*qn-1
Если q > 0 все члены геометрической прогрессии имеют один и тот же знак, совпадающий со знаком числа b.
Если q < 0 знаки членов геометрической прогрессии чередуются.

Изучение новой темы
Тема: Бесконечно убывающая геометрическая прогрессия. (записать в тетрадь)
Бесконечно убывающая геометрическая прогрессия — это прогрессия, у
которой |q| < 1.
Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма n первых членов рассматриваемой прогрессии при неограниченном возрастании числа n.
Формула суммы членов бесконечно убывающей геометрической прогрессии:
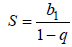 , где q ≠ 1
, где q ≠ 1
Задания с решениями записать в тетрадь
№ 1. Доказать, что геометрическая прогрессия является бесконечно убывающей:
1, 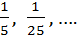
Доказательство: ищем знаменатель по формуле
 ,
,
q = 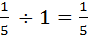 < 1, следовательно, геометрическая прогрессия - убывающая
< 1, следовательно, геометрическая прогрессия - убывающая
№ 2. Найти сумму бесконечно убывающей геометрической прогрессии
q= 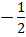 , b1 =
, b1 = 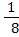
Решение: по формуле
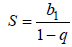
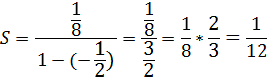
Ответ: 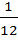
Выполнить задания самостоятельно и решения записать в тетрадь
№ 3. Доказать, что геометрическая прогрессия является бесконечно убывающей:
 ,
, 
№ 4. Найти сумму бесконечно убывающей геометрической прогрессии
q= 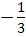 , b1 =
, b1 = 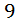
Спасибо за внимание!
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|