
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ковариантное или абсолютное дифференцирование тензоров.
Ковариантное или абсолютное дифференцирование тензоров.
Дифференциально-геометрические связности.
Символы Кристоффеля.
Мы настолько привыкли к “обычным” правилам дифференцирования, что сама мысль о том, что они могут быть изменены кажется странной. Однако такая надобность возникает, если мы хотим дифференцировать тензоры ненулевого ранга и притом так, чтобы они остались тензорами.
Начнём с того, что тензор, определённый в заданном базисе, начнёт изменяться в координатах, если базис будет “двигаться”. Изменение координат тензора очевидно, так движение базиса суть не что иное, как переход к новым базисам. В тензорной алгебре мы рассматривали только аффинные линейные преобразования. Для них вторые производные равнялись тождественно нулю. Что произойдёт, если преобразование достаточно гладкое, но не линейное? Например, движении по гладкой поверхности, заданной дважды дифференцируемым отображением. Мы выясним в последующем, что на такой поверхности определены симметрические первая и вторая квадратичные формы. Нас сейчас будет интересовать первая
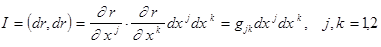 .
.
Как известно,в любой обыкновенной точке поверхности векторы 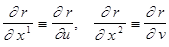 -линейно независимы. Поэтому они образуют базис в касательной плоскости к поверхности, по которой мы движемся. Обозначим этот базис:
-линейно независимы. Поэтому они образуют базис в касательной плоскости к поверхности, по которой мы движемся. Обозначим этот базис:
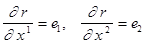 .Таким образом
.Таким образом 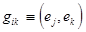 .Продифференцируем это тождество по переменной
.Продифференцируем это тождество по переменной 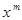 .
.
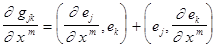 . (1)
. (1)
Вектор 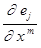 спроектируем на
спроектируем на 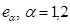 . Получим очень важное равенство
. Получим очень важное равенство
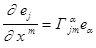 . (2)
. (2)
DEF 1. 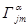 -символ Кристоффеля второго рода, или дифференциально-геометрическая связность, определённая в данном базисе на дважды дифференцируемой поверхности.
-символ Кристоффеля второго рода, или дифференциально-геометрическая связность, определённая в данном базисе на дважды дифференцируемой поверхности.
NB.Заметим, что по построению 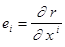 ,и, следовательно,
,и, следовательно, 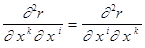 в силу теоремы о равенстве смешанных производных у дважды дифференцируемой функции. Поэтому символы Кристоффеля второго рода симметричны по нижним индексам
в силу теоремы о равенстве смешанных производных у дважды дифференцируемой функции. Поэтому символы Кристоффеля второго рода симметричны по нижним индексам
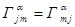 . (3)
. (3)
Из формулы (1) в силу (2) получим
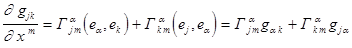 . (4)
. (4)
Поменяем в равенстве (4) индексы j и m местами.
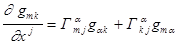 . (5)
. (5)
Ту же самую операцию проведём в (5) с индексами k и j.
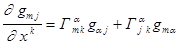 . (6)
. (6)
Запишем уравнения (4),(5),(6) в виде единой системы.
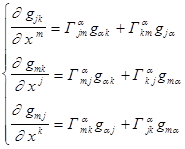 (7)
(7)
Если учесть, что метрический тензор симметричен: 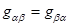 ,а символ Кристоффеля симметричен по нижним координатам, то складывая первые два уравнения в (7) и вычитая третье, получим:
,а символ Кристоффеля симметричен по нижним координатам, то складывая первые два уравнения в (7) и вычитая третье, получим:
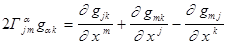 .
.
Умножая последнее равенство на 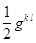 и учитывая тождество
и учитывая тождество 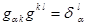 , окончательно получим:
, окончательно получим:
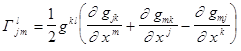 (8)
(8)
Из равенства (8) следует, что символы Кристоффеля являются функцией метрического тензора и его производных. В частности, в декартовых координатах 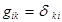 - кронекеровское, и, следовательно
- кронекеровское, и, следовательно 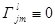 .
.
Теперь мы уже готовы к тому, чтобы продифференцировать тензоры типов (0,1) и (1,0).
DEF 1. 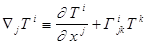 ,
,
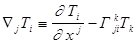 ,
,
называется ковариантными или абсолютными производными тензоров 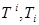 ,причём результат дифференцирования снова тензор типа (1,1) в первом случае и типа (2,0) во втором.
,причём результат дифференцирования снова тензор типа (1,1) в первом случае и типа (2,0) во втором.
Убедимся в том, что определение говорит правду в первой строчке формул. Иными словами, верна ли следующая цепочка тензорных равенств.
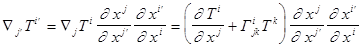 (9)
(9)
Установим прежде всего связь между символами Кристоффеля в старых и новых координатах. По определению
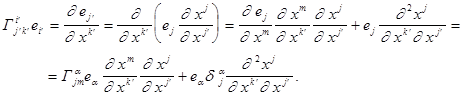
Теперь умножим обе части на 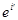 ,заметив при этом,что в силу формул Гиббса
,заметив при этом,что в силу формул Гиббса
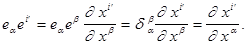
Получим окончательно.
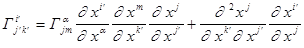 . (10)
. (10)
На очереди преобразование ‘’обычных’’ частных производных контравариантного одновалентного тензора.
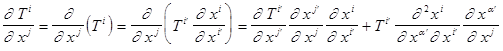 . (11)
. (11)
Осталось заметить, что при переходе к новому базису
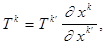 (12)
(12)
и преобразовать правую часть (9) с учётом формул (10),(11) и (12).
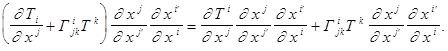
Хотя преобразования и громоздки,местами встречаются приятные моменты,учитывающие умножение якобианов взаимно-обратимых гладких отображений:
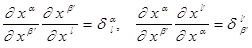 .
.
Продолжим наше путешествие по формулам.
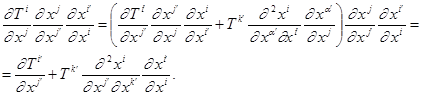
Здесь мы во втором члене в скобках поменяли индекс 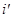 на
на 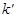 .Это можно так как по нему идёт свёртка, и это нужно, чтобы не вызвать путаницы - за скобкой снова встречается индекс
.Это можно так как по нему идёт свёртка, и это нужно, чтобы не вызвать путаницы - за скобкой снова встречается индекс 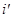 .
.
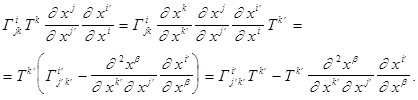
Осталось сложить полученные формулы и, заметив, что вторые слагаемые взаимоуничтожаются, получить
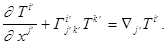
Что и требовалось доказать, а то что ковариантное дифференцирование ковариантного тензора первого ранга приводит к тензору типа (2,0) мы проверять не будем. В этом теперь вы можете убедиться и сами. Более того вы можете показать, что при ковариантном дифференцировании тензора типа (p,q) справедлива следующая , внешне страшноватая, но чудесная формула.
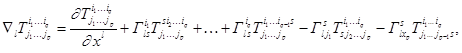
определяющая тензор типа (q,p+1).Легко проверить , что абсолютное дифференцирование сохраняет обычные правила дифференцирования
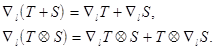
Теорема.Операция ковариантного дифференцирования и свёртки перестановочны.
Доказательство. Достаточно проверить утверждение на тензоре типа (1,1).
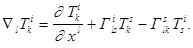
Положим в этом равенстве 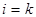 .Тогда слева стоит
.Тогда слева стоит 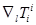 , равная обычной частной производной (
, равная обычной частной производной ( 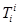 -тензор нулевого ранга - скаляр). Справа
-тензор нулевого ранга - скаляр). Справа 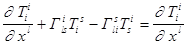 , так как
, так как 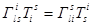 .Для тензоров более высокого ранга в доказательстве появляются добавочные взаимоуничтожающиеся члены.
.Для тензоров более высокого ранга в доказательстве появляются добавочные взаимоуничтожающиеся члены.
В заключение заметим, что ковариантное дифференцирование согласовано сримановой метрикой, то есть 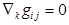 и
и 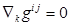 .Первое из этих равенств не что иное, как формула (4)
.Первое из этих равенств не что иное, как формула (4)
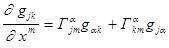 ,
,
полученная нами в самом начале лекции. Для доказательства второго возьмём ковариантную производную от произведения метрических тензоров
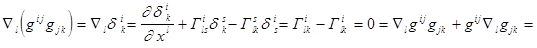
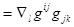 .Откуда в силу невырожденности
.Откуда в силу невырожденности 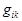 следует, что
следует, что 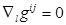 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|