Лабораторная работа № 1- 10. ИЗУЧЕНИЕ СТАЦИОНАРНОГО ТЕЧЕНИЯ ЖИДКОСТИ. В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. ВВЕДЕНИЕ

Лабораторная работа № 1- 10

ИЗУЧЕНИЕ СТАЦИОНАРНОГО ТЕЧЕНИЯ ЖИДКОСТИ

В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ

Цель работы: экспериментальная проверка применимости уравнения Бернулли для случая течения воды в трубе переменного сечения.

ВВЕДЕНИЕ

Движение жидкости называется течением, совокупность частиц движущейся жидкости – потоком. Графически течение изображается линиями тока, это линии, касательные к которым в каждой точке совпадают с вектором скорости жидкости в этой точке. Густота линий определяет величину скорости. Часть жидкости, ограниченная линиями тока, называется трубкой тока, жидкость, протекающая внутри трубки тока, называется струёй.

Течение жидкости называется установившимся (стационарным), если форма и расположение линий тока, а также значения вектора скорости в каждой её точке со временем не меняется.

Рассмотрим трубку тока (рис 1). Выберем два её сечения ( 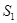и 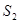), перпендикулярные направлению скорост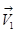и ( и ).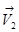

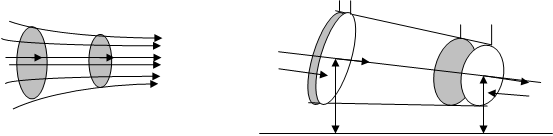
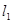
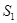
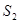
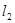
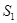
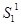
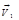
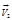
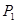
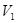
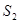
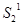
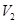
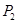
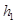
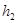
Рис. 1 Рис. 2

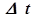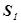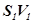
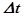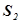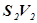
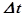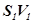
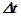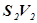
За время через сечение пройдет объём жидкости , через сечение : . Если жидкость несжимаема, то объёмы будут одинаковы: = =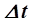const. Отсюда следует уравнение неразрывности (струи):

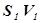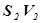= . (1)

Выделим в стационарно текущей идеальной жидкости (жидкость, где отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениям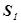и и 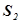(рис. 2). По трубке слева направо течет жидкость. В сечении 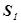скорость течения 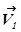, давление 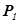, высота над линией отсчета - 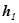. В сечении 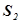скорость течения 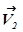, давление 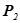, высота над линией отсчета - 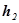. За малый промежуток времени 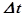жидкость перемещается от сечения 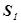к сечению 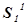и от сечения 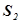к сечению .

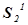Пусть работа, совершаемая при перемещении всей жидкости, заключенной между сечениям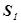и и 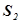за промежуток времени 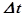равна А. При переносе жидкости на расстояние 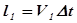совершается работа: 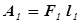, здесь: 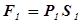. Для переноса жидкости на расстояние 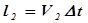совершается работа: 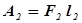, здесь 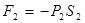. Следовательно:

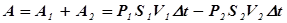. (2)

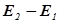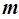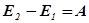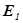Согласно закону сохранения энергии, изменение полной энергии идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы жидкости: , где и 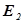- полные энергии жидкости массой 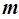в местах сечений. Полные энерги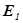и и 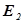есть сумма кинетической и потенциальной энергий:

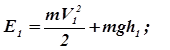
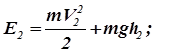(3)

Из (2) и (3) следует:

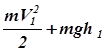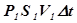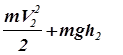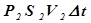+ = + (4)

Из уравнения неразрывности струи следует, что объём перемещенной жидкости остается постоянным, т.е.: 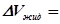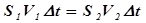. Разделив (4) на 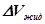, и учтя, что 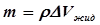, получим:

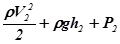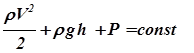, или . (5)

Для трубки, расположенной горизонтально, 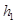= 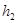, тогда:

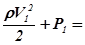
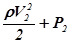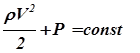, или . (6)

Уравнения (5) и (6) называются уравнением Бернулли - это закон сохранения энергии для установившегося течения идеальной жидкости. В этом уравнении величина Р, равная 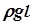( 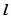-высота подъёма жидкости в манометрической трубке), называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела или на стенку трубки). Величина 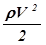называется динамическим давлением; 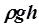- гидростатическое давление. Для горизонтальной трубки тока: 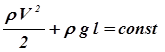- это полное давление.

Из уравнений (1) и (6) следует, что скорость течения жидкости в сечении 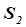равна:

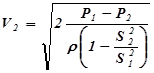. (7)

Поток жидкости определяется её объёмом, проходящим через поперечное сечение трубопровода в единицу времени, и выражается формулой: 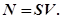Т.к. Р₁- Р₂= DР, то для сечения 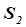имеем:

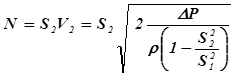. (8)

12 3 Следующая ⇒