Контакты

Случайная статья

Уважаемый студент, добрый день.

Уважаемый студент, добрый день.

Конспект и решения с ответами прислать на e-mail: altjin46@rambler.ru или в личку ВК.

Тема: Определённый интеграл.(записать в тетрадь)

Определенный интегралот функции 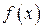, непрерывной на отрезке 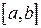, вычисляется по формул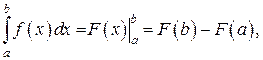е: где 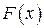— первообразная для функции 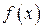, т. е.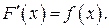

Формула называется формулой Ньютона — Лейбница.

Свойства определенного интеграла:

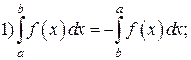
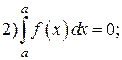
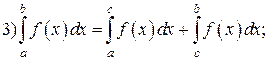
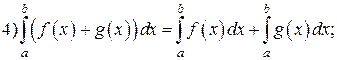
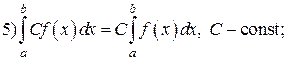
6) Если 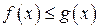для всех 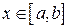, то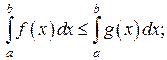

7) Если 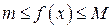для всех 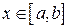, то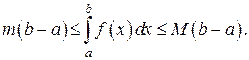

При вычислении определенного интеграла для нахождения первообразной используют те же методы, что и для нахождения неопределенного интеграла, т. е. замену переменной, интегрирование по частям и т. д. Однако есть ряд особенностей. При замене переменной по формуле необходимо в соответствии с заменой менять пределы интегрирования: 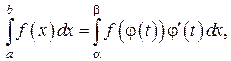где 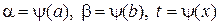— обратная к 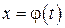функция.

Формула интегрирования по частям (3) приобретает вид: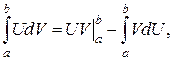

Задания с решениями и ответами записать в тетрадь

Вычислить определенные интегралы:

№ 1. 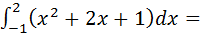[ x³+x²+x] 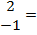[ 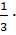2³+2²+2]- [ (-1)³+(-1)²+(-1)]=9

№ 2

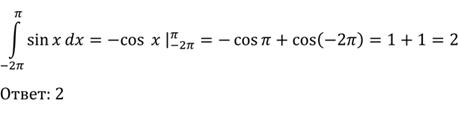
№ 3. (методом замены переменных)

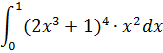
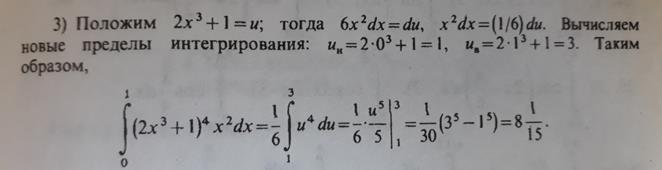
№ 4. (интегрирование по частям)

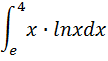
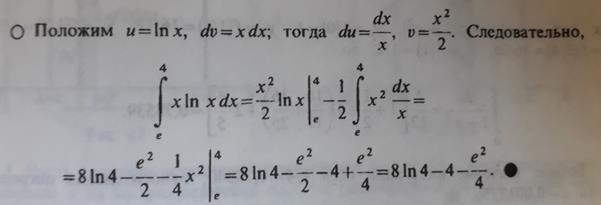
Выполнить задания самостоятельно

Вычислить определенные интегралы:

№ 5. (методом замены переменных)

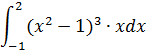
№ 6. (интегрирование по частям)

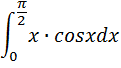
Спасибо за внимание!

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.