
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Первообразная
- Рассмотреть теорию, формулы, примеры решения, правила нахождения первообразных, выполнить предложенное после них задание.
- Выполненное домашнее задание можно направлять на мою электронную почту или в контакте, можно в виде фото листа тетради. Степанова Л.В.-адрес электронной почты: lora01051966@mail.ru
Первообразная
Определение. Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x).
Основное свойство первообразных.
Если F (x) – первообразная функции f (x), то и функция F (x)+ C , где C –произвольная постоянная, также является первообразной функции f (x) (т.е. все первообразные функции f(x) записываются в виде F(x) + С ).
Таблица первообразных.
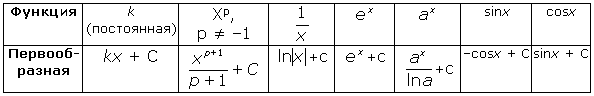
| функция | (кх+в)р | 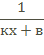
| екх+в | Sin(kx+b) | Cos(kx+b) |
| Первооб- разная | 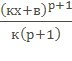 +С +С
| 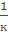 ln(кх+в) +С ln(кх+в) +С
| 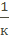 екх+в +С екх+в +С
| - 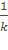 Cos(kx+b)+C Cos(kx+b)+C
| 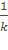 sin(kx+b)+C sin(kx+b)+C
|
Правила нахождения первообразных.
Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:
1. F ( x ) ± G ( x ) – первообразная для f ( x ) ± g ( x );(первообразная алгебраической суммы равна алгебраической сумме первообразных).
2. а F ( x ) – первообразная для а f ( x ); (постоянная (числовой коэффициент) выносится на знак первообразной).
3. 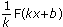 – первообразная для f (kx + b ).(Коэффициент, стоящий перед х выносится за знак первообразной обратным числом). Например: 6 – как
– первообразная для f (kx + b ).(Коэффициент, стоящий перед х выносится за знак первообразной обратным числом). Например: 6 – как 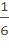 .
.
Примеры:- найти все первообразные.
1) 4, F(x)= 4х+С
2) 3х5+4х3, F(x)=  +
+ 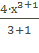 +С =
+С = 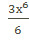 +
+ 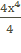 + С =
+ С = 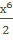 + х4 +С
+ х4 +С
3)  -
-  преобразуем вначале 2х-3 - 3
преобразуем вначале 2х-3 - 3 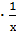 . теперь находим первообразную
. теперь находим первообразную
F(x) = 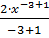 – 3lnx +C=
– 3lnx +C= 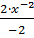 -3lnx +C = -x-2 -3lnx +C =-
-3lnx +C = -x-2 -3lnx +C =- 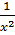 – 3lnx +C
– 3lnx +C
4) (x-2)3, F(x)= 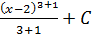 =
= 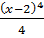 +C
+C
5) e4x+1, F(x)= 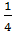 e4x+1 +C (коэффициент, стоящий перед х выносится обратным числом –в 5,6,7,8 примерах)
e4x+1 +C (коэффициент, стоящий перед х выносится обратным числом –в 5,6,7,8 примерах)
6) sin (8x-6), F(x)= 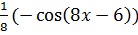 +C= -
+C= - 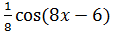 +C
+C
7) cos(2x+7), F(x) =  sin(2x+7)+C
sin(2x+7)+C
8) cos(  x+7), F(x) = 2sin(2x+7)+C
x+7), F(x) = 2sin(2x+7)+C
= Выполнить самостоятельную работу: - найти все первообразные
1) 2х5 – 3х2
2) 5х4+ 2х3
3)  +
+ 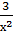
4) 3cosx – 4sinx
5) ex – 2cosx
6) (x+1)4
7) cos(3x+4)
8) e3x – 5
9) 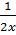
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|