Свойства определенного интеграла.

Лекция от 21.04. Определенный интеграл и его свойства.

Основная часть материалов этой лекции содержится в пособии “Математический анализ” (файл Мат.ан.2013.pdf), разделы 6.1 и 6.2, стр. 47 – 52. От себя добавляю лишь некоторые пояснения и комментарии.

Пусть на замкнутом отрезке 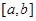задана кусочно-непрерывная функция 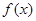(см. Определение 6.4 пособия). Тогда можно определить число, которое называется определенным интегралом от этой функции по отрезку 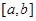и обозначается .

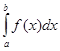Это число имеет следующий геометрический смысл. Рассматривается площадь фигуры, ограниченной осью OX на отрезке 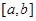и графиком функции. На интервалах, где 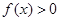, эта площадь берется со знаком “+”, на остальных интервалах – со знаком “-”. 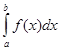равен сумме получившихся площадей. Так, например, 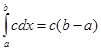(площадь прямоугольника), 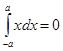(разность площадей двух равных треугольников).

В большинстве случаев, когда график функции не является прямой линией, вычислить интеграл через площадь удается только приближенно, разбив фигуру на много узких прямоугольников. Чем уже прямоугольники, тем ближе сумма их площадей приближается к точному значению площади фигуры, а значит и интеграла. На этом и основывается строгое определение определенного интеграла - см. определения 6.1 – 6.3 пособия. Фактически определение 6.3 можно кратко записать следующим образом:

= .

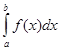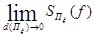Теоремы существования и единственности определенного интеграла (Теоремы 6.1 и 6.2 пособия) можно принять без доказательств.

Свойства определенного интеграла.

Свойство линейности. Это свойство сформулировано в Теореме 6.3 пособия. Оно фактически вытекает из свойств линейности суммы и предела. Приведенное в пособии подробное доказательство можно пропустить.

Свойство аддитивности. Это свойство сформулировано в Теореме 6.4 пособия. Оно фактически следует из геометрического смысла определенного интеграла. (Без точного доказательства.)

Свойство монотонности. Это свойство сформулировано в Теореме 6.5 пособия. Оно может быть обосновано с помощью предельного перехода в неравенстве. Приведенное в пособии подробное доказательство можно пропустить. Важным следствием этого свойства является тот факт, что модуль интеграла не превосходит интеграла от модуля функции – см. Следствие 6.2 пособия (с доказательством).

Теорема о среднем – см. Теорему 6.6 пособия (с доказательством).

Понятие определенного интеграла легко обобщается на случай, когда верхний предел меньше нижнего – см. Определение 6.5 пособия.

Дополнительное замечание. При вычислении определенных интегралов иногда оказываются полезными следующие свойства интегралов по симметричному отрезку .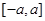

Если 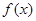- четная, то .

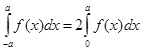Если 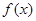- нечетная, то .

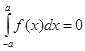Эти свойства вытекают из геометрического смысла интеграла.