Уважаемый студент, добрый день.

Уважаемый студент, добрый день.

Конспект и задания с решениями и ответами прислать на на e-mail: altjin46@rambler.ru или в личку ВК.

В тетрадь записываем число и свою фамилию собственноручно!

Ответьте на вопрос письменно: как называется график функции f(x)=х², и зарисовать его схематично.

изучение новой темы

Тема " Интеграл. Площадь криволинейной трапеции "(записать в тетрадь)

Приготовьте карандаш и линейку!

Таблица первообразных (в таблице 10 формул) (не записывать в тетрадь)

Запишем 11формулу: С - произвольная постоянная, её первообразная F(x)=Cx

Рассмотрим график функции f (x) на некотором промежутке [a;b]

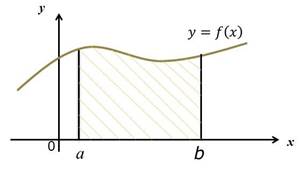Определение. Криволинейная трапеция (заштрихованная область) - это фигура, ограниченная сверху графиком функции

f(x), снизу отрезком [a;b]. с боков прямыми х = a, х = b.

Площадь криволинейной трапеции можно вычислить по формуле (2)

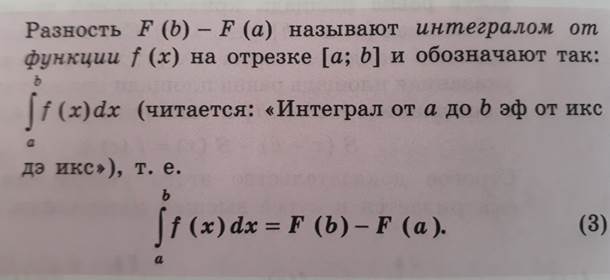
a - нижний предел интегрирования, b - верхний предел интегрирования , dx - знак дифференциала

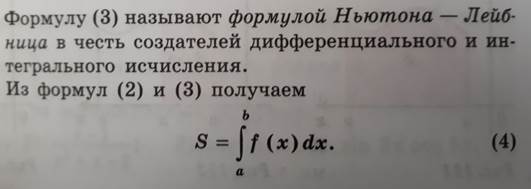
Задания с решениями записать в тетрадь

№ 1. Найти площадь криволинейной трапеции, ограниченной прямыми a=-2, b=1, осью Ох и графиком функции f(x)=х²+1.

Решение: строим график функции f(x)=х²+1- парабола

1. Находим вершину параболы (x₀; y₀) параболы по формулам: 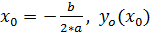Функцию приравняем к нулю, т.е. если 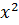+1=0, тогда выпишем коэффициенты

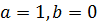
Следовательно, 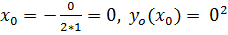+1=1

2. Вычислим и запишем в таблицу координаты

x	-3	-2	-1
y

3. Построим криволинейную трапецию: сначала нарисуем параболу, затем прямые х=-2, х=1,

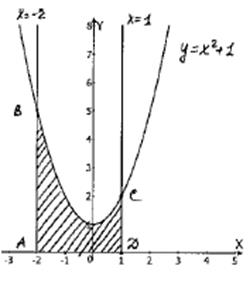Заштрихованная область ABCD - криволинейная трапеция
4. Площадь находим по формуле: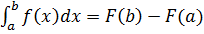

S_ABCD= 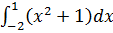=(находим первообразную функции 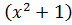по таблице и вместо знака интеграла ставим вертикальную прямую и указываем пределы интегрирования ) = 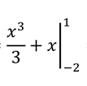= (подставляем верхний, а затем нижний пределы вместо х, между ними знак минус) = 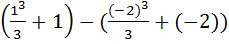= 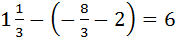(кв.ед.)

Ответ: S_ABCD= 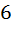(кв.ед.)

Выполнить задания самостоятельно

№ 2. Найти площадь криволинейной трапеции, ограниченной прямыми a=3, b=4, осью Ох и графиком функции f(x)=х².

Спасибо за внимание!