Занятие 91. Домашняя работа. luda181929@yandex.ru. Отправляемым архивным файлам даёте имя «фамилия, группа, дата занятия». Например: ПетроваИСП-О-19 12.04

Занятие 91

Тема: Наибольшее и наименьшее значения функций.

Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:

· Найти производную функции.

· Определить критические точки (те точки, в которых производная функции обращается в ноль или не существует).

· Выбрать из найденных точек те, которые принадлежат данному отрезку.

· Вычислить значения функции (не производной!) в этих точках и на концах отрезка.

· Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.

Пример Найдите наименьшее и наибольшее значения функции y = x³ – 18x² + 81x + 23 на отрезке [8; 13].

Решение:действуем по алгоритму нахождения наименьшего и наибольшего значений функции на отрезке:

1. y’ = 3x² – 36x + 81.

2. y’ = 3x² – 36x + 81 = 0

x² – 12x + 27 = 0,

x = 3 и x = 9

х = 3 не принадлежит данному отрезку

3. x = 9 [8; 13].

4. y = x³ – 18x² + 81x + 23 = x(x-9)²+23:

o y(8) = 8 · (8-9)²+23 = 31;

o y(9) = 9 · (9-9)²+23 = 23;

o y(13) = 13 · (13-9)²+23 = 231.

Ответ: наименьшее значение у=23, наибольшее у=231.

Домашняя работа

Найдите наибольшее и наименьшее значения функции на отрезке:

1) у = ,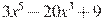

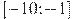
2) ,

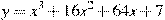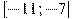
3) ,

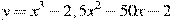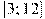
luda181929@yandex.ru

В работе указывайте ФИО и группу

Отправляемым архивным файлам даёте имя «фамилия, группа, дата занятия». Например: ПетроваИСП-О-19 12.04