
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольные вопросы. 4. ПОЗИЦИОННЫЕ ЗАДАЧИ
В случае когда поверхность занимает проецирующее положение (рис. 166), следует учитывать следующие обстоятельства:
1. Если заданная проекция точки принадлежит невырожденной проекции поверхности, то решение задачи упрощается. Достаточно провести через эту проекцию точки линию связи и пересечь ее с вырожденной проекцией поверхности.
2. Если заданная проекция точки принадлежит вырожденной проекции поверхности, то задача решения не имеет.
Рис. 166. Построение точки М поверхности проецирующей
по заданной проекции М1 (эпюр Монжа)
Задача 5. На модели поверхности дана одна проекция линии l, которая является ее плоским сечением. Построить другую проекцию этой линии.
Наиболее востребованными являются сечения, полученные проецирующей плоскостью, поэтому рассмотрим только этот вариант.
Алгоритм построения модели плоского сечения поверхности по одной заданной проекции имеет следующие операции:
1. Определить, какое плоское сечение поверхности представляет собой искомая линия.
2. Выявить ее характерные и, если необходимо, случайные точки.
3. Построить искомые проекции выявленных точек. Для чего необходимое количество раз решить задачу 3 этого раздела. Соединить полученные точки с учетом сведений, полученных в п. 1.
4. Установить видимый и невидимый участки построенной линии.
На рис. 167 – 176 приведены примеры нескольких вариантов построения линии l, принадлежащей поверхности, если дана одна ее проекция. Она получена от сечения поверхности проецирующей плоскостью.
Чтобы реализовать первый пункт алгоритма, необходимо знание плоских сечений поверхностей.
Плоские сечения поверхностей:
1. Коническая поверхность, у которой в качестве направляющей окружность или эллипс, имеет следующие плоские сечения:
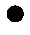 Гипербола образуется, если секущая плоскость параллельна двум образующим поверхности (рис. 161). При этом вторая ветвь гиперболы возникает на другой части конуса. В данном случае – на обратном конусе.
Гипербола образуется, если секущая плоскость параллельна двум образующим поверхности (рис. 161). При этом вторая ветвь гиперболы возникает на другой части конуса. В данном случае – на обратном конусе.
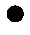 Парабола возникает, когда секущая плоскость параллельна одной образующей конуса (рис. 162).
Парабола возникает, когда секущая плоскость параллельна одной образующей конуса (рис. 162).
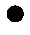 Окружность или эллипс получаются при пересечении плоскостью всех образующих конической поверхности (рис. 163).
Окружность или эллипс получаются при пересечении плоскостью всех образующих конической поверхности (рис. 163).
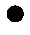 Две прямые выделяют на поверхности плоскость, которая проходит через вершину конической поверхности (рис. 164).
Две прямые выделяют на поверхности плоскость, которая проходит через вершину конической поверхности (рис. 164).
2. Цилиндрическая поверхность, у которой в качестве направляющей окружность или эллипс, имеет следующие плоские сечения:
 Окружность или эллипс получаются при пересечении плоскостью всех образующих цилиндрической поверхности (рис. 165).
Окружность или эллипс получаются при пересечении плоскостью всех образующих цилиндрической поверхности (рис. 165).
 Две прямые выделяет на поверхности плоскость, которая проходит через вершину цилиндрической поверхности (рис. 166).
Две прямые выделяет на поверхности плоскость, которая проходит через вершину цилиндрической поверхности (рис. 166).
3. Любое сечение сферы плоскостью представляет собой окружность (рис. 168, 169).
5. Плоское сечение многогранника – многоугольник (рис. 169, 170).
Характерные точки линии поверхности – это точки, которые принадлежат очеркам и ребрам поверхностей. Остальные точки, определяющие линию, называются случайными или промежуточными.
Если заранее известно, какая линия окажется в сечении поверхности, то, как правило, для построения искомой проекции линии достаточно только опорных точек (рис. 167, 170, 173, 175, 176). Если необходимо уточнить искомую проекцию линии, то выбирают еще случайные точки (рис. 169, 174). При построении проекции линии на многограннике необходимо взять точки только на его ребрах и построить их другие проекции (рис. 175, 176).
Рис. 167. Построение гиперболыl, которая лежит на поверхности конуса, по заданной проекцииl1 (перспектива)
Рис. 168. Построение параболыl, которая лежит на поверхности конуса, по заданной проекцииl2 (эпюр Монжа)
Рис. 169. Построение окружности l и эллипсаl, которые лежат на поверхности конуса, по заданной проекцииl2 (эпюр Монжа)
Рис. 170. Построение прямыхl, которые лежат на поверхности конуса, по заданной проекцииl1 (эпюр Монжа)
Рис. 171. Построение окружностиl и эллипса l, которые лежат на поверхности цилиндра, по заданной проекцииl2 (эпюр Монжа)
Рис. 172. Построение прямыхl, которые лежат на цилиндрической поверхности, по заданной проекцииl1(перспектива)
Рис. 173. Построение окружностиl, которая лежит на поверхности сферы, по заданной проекцииl1 (перспектива)
Рис. 174. Построение модели окружностиl, которая лежит на поверхности сферы, по заданной проекцииl2 (эпюр Монжа)
заданной проекцииl1 (перспектива)
Рис. 175 Построение многоугольника l, который лежит на поверхности пирамиды, по заданной проекцииl1 (эпюр Монжа)
При построении линии на проецирующей поверхности следует учитывать, что проекция любой ее линии тождественно совпадает с вырожденной проекцией поверхности (рис. 176).
Рис. 176. Построение многоугольника l, который лежит на поверхности призмы, по заданной проекцииl1 (эпюр Монжа)
В рассмотренных примерах линии строились с использованием характерных точек. Случайные точки, как правило, не требуются, если заранее известно, как выглядит плоское сечение. Построение этих точек осуществлялось с помощью решения задачи 3 этого раздела.
Видимый и невидимый участки построенной линии разделяются точками лежащими на очерках.
Контрольные вопросы
1. Что называется очерком поверхности?
2. Дайте определение модели поверхности.
3. Перечислить задачи, из решения которых складывается работа с моделью поверхности.
4. В каких случаях поверхность может занимать частное положение?
5. Почему модель сферы в перспективе и аксонометрии считаются приближенными?
6. Как называются очерки сферы при моделировании ее на эпюре Монжа?
7. Какие линии считаются графически простыми?
8. Перечислитьоперации алгоритма по построению проекции точки, если она принадлежит промоделированной поверхности и дана одна ее проекция?
9. В каких случаях алгоритм по построению проекции точки, если она принадлежит промоделированной поверхности и дана одна ее проекция, упрощается?
10. Перечислить плоские сечения конуса и указать при каких условиях они возникают.
11. Перечислить плоские сечения цилиндра и указать при каких условиях они возникают.
12. Что является плоским сечением сферы?
13. Что является плоским сечением многогранника?
14. Перечислить опорные точки линии, которые принадлежат линии поверхности.
4. ПОЗИЦИОННЫЕ ЗАДАЧИ
Работа с геометрическими моделями, как было сказано выше, складывается из решения позиционных и метрических задач. Причем на практике чаще всего приходится иметь дело с позиционными задачами. Они являются также основой при решении метрических задач и построения теней на моделях различных объектов. Это условие определяет доминирующий характер позиционных задач в курсе начертательной геометрии. Общая характеристика и классификация позиционных задач была дана в разделе 2.
Позиционными задачами называют такие, которые позволяют определить взаимную принадлежность или неприналежность геометрических элементов друг другу или выявить третий элемент, возникающий как следствие взаимного расположения двух других элементов.
В зависимости от числа элементов, между которыми устанавливаются позиционные характеристики, все позиционные задачи делятся на две группы задач, где:
1) Выясняется взаимная принадлежность двух элементов друг другу;
2) Выявляется третий элемент как результат расположения двух данных элементов. В этой группе выделяют следующие подгруппы:
· задачи на пересечение;
· задачи на объединение элементов.
Примером первой группы задач являются задачи на определение принадлежности прямой плоскости или поверхности, принадлежности точки прямой, плоскости или поверхности. Примером второй группы позиционных задач являются задачи на пересечение прямой с плоскостью или поверхностью, пересечение поверхностей, проведение прямой через две точки или плоскости через три точки и т. п. Очевидно, что для решения задач на объединение не требуется знания специальных приёмов. Но когда дана задача на пересечение, то для поиска общего элемента двух заданных геометрических элементов необходимо выполнить специальные построения. Основными задачами этой группы являются задачи по определению точки пересечения прямой с плоскостью или поверхностью. Умение решать их позволит осуществлять решение более сложных: пересечение плоскостей и пересечение поверхностей. Причем последняя требует умения решать все остальные, которые в той или иной комбинации позволяют найти общую линию двух и более поверхностей. Следует заметить, что задачи на объединение элементов участвуют как базовые в решении всей группы задач на пересечение. В рис. 200 отражена взаимозависимость всех групп позиционных задач.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|