
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРИМЕНЕНИЕ МЕТОДА ПЕРЕМЕЩЕНИЙ. К РАСЧЕТУ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
ПРИМЕНЕНИЕ МЕТОДА ПЕРЕМЕЩЕНИЙ
К РАСЧЕТУ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ
Методические указания
к выполнению расчетно-графической работы
по курсу «Строительная механика»
для студентов специальностей 291100, 291000, 290300, 290600
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2009
ВВЕДЕНИЕ
Известно, что при расчете упругих статически неопределимых стержневых систем методом сил [1, 2, 3] за лишние неизвестные принимаются усилия в «лишних» связях (силы и моменты). После нахождения лишних неизвестных определяются внутренние усилия в любом сечении системы и затем линейные и угловые перемещения в произвольной точке системы. Таким образом, при расчете упругих стержневых систем по методу сил определение усилий предшествует определению перемещений.
Метод перемещений, называемый также методом деформаций, предусматривает для упругих стержневых систем сначала нахождение угловых и линейных перемещений узлов статически неопределимых систем, а затем соответствующего им распределения внутренних усилий. При этом, как и в методе сил, для деформированного состояния стержневой системы принимаются следующие допущения [1, 2, 3]:
1) не учитывается влияние продольных N и поперечных Q сил на пере-
мещения узлов системы, что, в частности, соответствует гипотезе о нерастяжимости и несжимаемости всех ее стержней ( 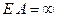 ),
),
2) расстояния между узлами системы при деформации изгиба прямоли-
нейных стержней не изменяются,
3) углы поворота сечений системы по малости принимаются равными
тангенсам данных углов,
4) концы стержней, сходящихся в жестком узле системы, поворачива-
ются при деформации системы на одинаковый угол.
Метод перемещений получил большое распространение при расчете сложных многократно статически неопределимых систем с малой подвижностью узлов, к которым относятся фермы с жесткими узлами, сложные каркасные рамы, жесткие пространственные стержневые системы. При этом число неизвестных по методу перемещений, как правило, существенно меньше числа неизвестных по методу сил, что наглядно демонстрирует выгоды использования метода перемещений в расчетах статически неопределимых систем с большим числом «лишних» связей.
Ценность алгоритма метода перемещений состоит также и в том, что на его основе предложен ряд приближенных методов расчета статически неопределимых систем и созданы современные модификации метода конечных элементов (МКЭ), приспособленные для расчета современных стержневых, плоских, оболочечных и пространственных конструкций.
В настоящее время известны две формы решения задач по методу перемещений: каноническая и развернутая. Представленная в указаниях каноническая форма метода перемещений аналогична канонической форме записи уравнений метода сил [1, 2, 3] и развита в трудах отечественных ученых А.А. Гвоздева, И.М. Рабиновича и А.Ф. Смирнова.
ЦЕЛЬ РАБОТЫ
Объектом исследования является метод перемещений в применении для расчета статически неопределимых рам на силовые воздействия, изменения температурного режима и осадки опор.
В процессе выполнения работы:
- изучается методика определения числа неизвестных по методу перемещений (степени кинематической неопределимости рамы);
- изучается методика образования основной системы метода перемещений;
- изучаются вопросы составления канонических уравнений метода перемещений;
- изучаются вопросы построения «единичных» и «грузовых» эпюр изгибающих моментов в основной системе метода перемещений;
- изучаются вопросы вычисления коэффициентов канонических уравнений метода перемещений и их проверки;
- изучаются вопросы построения расчетных эпюр внутренних усилий M, Q, N в статически неопределимой раме и их проверки;
- изучаются вопросы определения перемещений в статически неопределимой раме;
- изучаются вопросы использования симметрии рам для упрощения их расчета по методу перемещений;
- изучаются вопросы расчета рам с наклонными стойками.
ЗАДАНИЕ НА РАБОТУ
Для статически неопределимой рамы требуется провести расчеты по методу перемещений на силовые воздействия, на изменения температурного режима и на осадки опор, предусматривающие выполнение следующих пунктов задания:
1) определение степени кинематической неопределимости рамы, равной числу неизвестных по методу перемещений,
2) образование основной системы метода перемещений,
3) составление канонических уравнений метода перемещений,
4) построение в основной системе эпюр изгибающих моментов 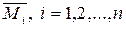 от единичных перемещений
от единичных перемещений 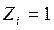 ,
,
5) построение в основной системе эпюр изгибающих моментов 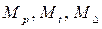 от заданных силовых нагрузок, изменения температурного режима и осадок опор,
от заданных силовых нагрузок, изменения температурного режима и осадок опор,
6) подсчет величин коэффициентов канонических уравнений 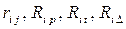 и их проверки,
и их проверки,
3
7) решение системы канонических уравнений метода перемещений для определения величин искомых угловых и линейных перемещений узлов 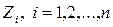 и проверка полученных значений,
и проверка полученных значений,
8) построение расчетных эпюр внутренних усилий M, Q, N от заданной силовой нагрузки,
9) выполнение проверок расчетных эпюр M, Q, N,
10) определение перемещений в заданных сечениях статически неопределимой рамы.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Условимся называть степенью кинематической неопределимости «n» число неизвестных узловых перемещений системы, знание которых позволяет полностью определить деформированное состояние системы. Для упругих систем это дает возможность определить также все усилия.
Степень кинематической неопределимости определяется по формуле:
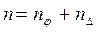 , (1)
, (1)
где 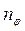 равно числу углов поворота жестких внеопорных узлов рамы, а
равно числу углов поворота жестких внеопорных узлов рамы, а 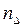 равно числу независимых линейных смещений узлов рамы.
равно числу независимых линейных смещений узлов рамы.
Жесткими являются такие узлы рамы, в которых концы не менее двух сходящихся в нем стержней соединены сваркой или спайкой (рис. 1).
Рис. 1
С учетом допущения о нерастяжимости и несжимаемости стержней рамы, что соответствует бесконечно большой величине жесткости стержней на растяжение-сжатие  , линейные перемещения узлов рамы, расположенных на одном стержне, будут линейно зависимыми.
, линейные перемещения узлов рамы, расположенных на одном стержне, будут линейно зависимыми.
Для определения величины  во все жесткие узлы рамы, в том числе и опорные, вводятся полные шарниры. Степень свободы полученного механизма совпадает с величиной
во все жесткие узлы рамы, в том числе и опорные, вводятся полные шарниры. Степень свободы полученного механизма совпадает с величиной  и может быть подсчитана по формуле:
и может быть подсчитана по формуле:
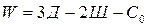 , (2)
, (2)
где Д – число «дисков» (стержней), Ш – число «простых» шарниров, объединяющих два диска (стержня),  – число опорных стержней системы.
– число опорных стержней системы.
Следует помнить, что полный (сложный) шарнир, соединяющий шарнирно в узле концы «к» дисков (стержней), эквивалентен «к-1» простому шарниру, объединяющему в узле лишь два стержня рамы.
Кроме того, при введении шарниров в узлы рамы все статически определимые консоли рамы необходимо предварительно отбросить.
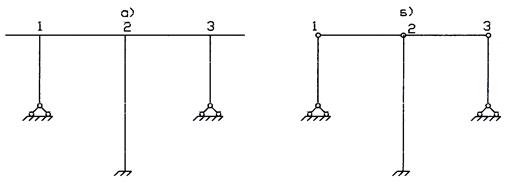
Рис. 2
Например, для рамы (рис. 2 а) преобразованная схема приведена на рис. 2 б и включает в себя:
1) Д = 5 – пять дисков (с учетом двух отброшенных консолей),
2) Ш = 4 – четыре «простых» шарнира (с учетом объединения слож-
ным шарниром в узле «2» трех дисков),
3)  = 6 – шесть опорных стерженьков (по два в каждой шарнирно-
= 6 – шесть опорных стерженьков (по два в каждой шарнирно-
неподвижной опоре).
В результате по формуле (2) получаем степень свободы преобразованной системы равной
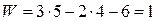 ,
,
что соответствует возможности линейного горизонтального смещения узлов 1, 2, 3 на одну и ту же величину, так как по допущению «1» жесткость всех стержней рамы на растяжение и сжатие бесконечно велика ( 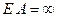 ).
).
Таким образом, выявлено, что для рамы с рис. 2 а величина 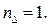 Так как данная рама включает в себя три жестких внеопорных узла, то для нее величина
Так как данная рама включает в себя три жестких внеопорных узла, то для нее величина  а общее число неизвестных по методу перемещений равно:
а общее число неизвестных по методу перемещений равно:
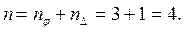
Данная величина n равна степени кинематической неопределимости исходной системы, то есть сумме общего числа независимых угловых перемещений жестких узлов рамы и общего числа независимых поступательных перемещений узлов рамы.
5
Для образования основной системы метода перемещений в исходную систему необходимо ввести « 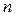 » дополнительных связей, устраняющих как угловые, так и линейные смещения узлов рамы. Данные связи бывают двух типов:
» дополнительных связей, устраняющих как угловые, так и линейные смещения узлов рамы. Данные связи бывают двух типов:
1) отдельные стержни устраняют линейные смещения узлов и изобра-
жаются на схемах в виде вертикальных или горизонтальных опорных стерженьков,
2) «шайбы», эквивалентные «плавающим» заделкам, не допускающим
поворота узлов, устраняют их угловые перемещения, не влияя на линейные смещения узлов, и изображаются на схемах в виде квадрата (  ).
).
Введение « 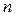 » перечисленных дополнительных связей превращает исходную систему в набор независимо деформирующихся стержней, различным образом закрепленных по концам и представленных на рис. 3.
» перечисленных дополнительных связей превращает исходную систему в набор независимо деформирующихся стержней, различным образом закрепленных по концам и представленных на рис. 3.

Рис. 3
Например, для рамы (рис. 4 а) со степенью кинематической неопределимости  основная система метода перемещений приведена на рис. 4 б, где дана также и нумерация дополнительных связей.
основная система метода перемещений приведена на рис. 4 б, где дана также и нумерация дополнительных связей.
Рис. 4
Следует помнить, что в исходной статически неопределимой системе перемещения конкретного сечения любого стержня вызывают перемещения всех сечений других стержней за счет угловых и линейных смещений узлов системы. В отличие от этого в основной системе метода перемещений деформации каждого стержня независимы от деформаций других стержней, что существенно облегчает расчет статически неопределимой системы.
Для составления канонической системы уравнений метода перемещений на основную систему необходимо наложить условия эквивалентности работы с исходной системой. Так как в исходной системе имеют место повороты и поступательные смещения узлов, то основной системе надо задать такие же повороты и смещения. Тогда реакции во всех дополнительно введенных « 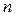 » связях основной системы, сопротивляющихся поворотам и смещениям, будут равны нулю, что даст систему уравнений вида:
» связях основной системы, сопротивляющихся поворотам и смещениям, будут равны нулю, что даст систему уравнений вида:
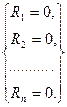 . (3)
. (3)
Запись уравнений (3) соответствует полной эквивалентности напряженно-деформированных состояний основной и исходной систем.
На основе использования принципа суперпозиции (независимости действия сил) уравнения (3) можно переписать в развернутом виде:
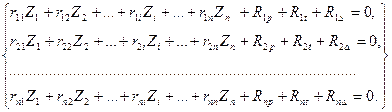 , (4)
, (4)
где 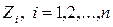 – неизвестные метода перемещений,
– неизвестные метода перемещений,  реакция в i-й дополнительной связи от единичного перемещения
реакция в i-й дополнительной связи от единичного перемещения 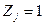 j-й дополнительной связи,
j-й дополнительной связи,  соответственно реакции в i-й дополнительной связи от внешней нагрузки, изменения температуры и осадки опор.
соответственно реакции в i-й дополнительной связи от внешней нагрузки, изменения температуры и осадки опор.
Для определения величин коэффициентов уравнений (4) необходимо построить в основной системе метода перемещений эпюры изгибающих моментов 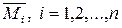 от единичных перемещений
от единичных перемещений 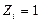 , а также эпюры изгибающих моментов
, а также эпюры изгибающих моментов 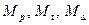 от силовых нагрузок, изменения температурного режима и осадок опор. При построении данных эпюр используются результаты решения типовых задач для статически неопределимых стержней, подвергнутым всем возможным воздействиям при любых возможных типах закреплений по концам. Данные результаты получены по методу сил и приведены в приложении к методическим указаниям.
от силовых нагрузок, изменения температурного режима и осадок опор. При построении данных эпюр используются результаты решения типовых задач для статически неопределимых стержней, подвергнутым всем возможным воздействиям при любых возможных типах закреплений по концам. Данные результаты получены по методу сил и приведены в приложении к методическим указаниям.
Необходимо отметить, что приведенные в приложении реактивные усилия по концам данных стержней записаны через погонные изгибные жесткости стержней, подсчитываемые по формуле:
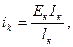 (5)
(5)
где 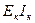 – изгибная жесткость «к» – го стержня,
– изгибная жесткость «к» – го стержня, 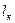 – его длина.
– его длина.
Кроме того, погонные изгибные жесткости всех стержней основной системы необходимо выразить через базовую (основную) погонную жесткость одного из стержней по формуле:
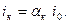 (6)
(6)
Это позволяет выразить все узловые реакции и моменты в основной системе от действия единичных перемещений 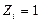 через величину
через величину 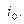
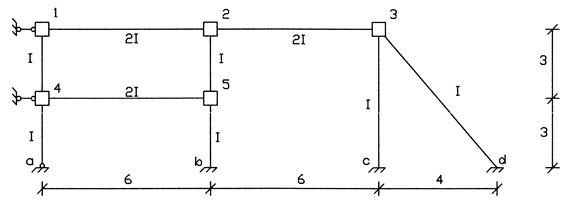
Рис. 5
Например, для основной системы метода перемещений (рис. 5) с учетом длины наклонной стойки «3 – d», равной 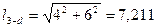 (м),
(м),
величины погонных изгибных жесткостей стержней будут равны:

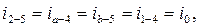
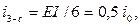
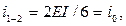
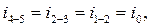
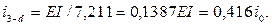
Далее необходимо изобразить деформационные схемы основной системы метода перемещений от единичных смещений 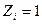 ,
,  , что позволит выявить расположение растянутых волокон всех стержней.
, что позволит выявить расположение растянутых волокон всех стержней.
Затем требуется построить эпюры «единичных» изгибающих моментов  от единичных перемещений
от единичных перемещений 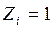 . При этом используются результаты решения типовых задач для статически неопределимых стержней, приведенные в приложении к указаниям.
. При этом используются результаты решения типовых задач для статически неопределимых стержней, приведенные в приложении к указаниям.
Следует помнить, что ординаты данных табличных эпюр для конкретного «к» - го стержня необходимо умножить на соответствующий ему коэффициент 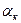 в формуле (6). Эпюры «единичных» изгибающих моментов
в формуле (6). Эпюры «единичных» изгибающих моментов
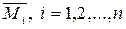 дают возможность подсчитать величины всех коэффициентов
дают возможность подсчитать величины всех коэффициентов 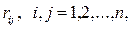 при неизвестных
при неизвестных 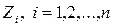 в уравнениях (4).
в уравнениях (4).
Для подсчета в уравнениях (4) величин 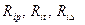 , являющихся соответственно реакциями в i-й дополнительной связи от действия внешней нагрузки, изменения температурного режима и осадки опор, в основной
, являющихся соответственно реакциями в i-й дополнительной связи от действия внешней нагрузки, изменения температурного режима и осадки опор, в основной
системе метода перемещений необходимо построить «грузовые» эпюры изгибающих моментов от соответствующих воздействий. При этом вновь необходимо использовать приведенные в приложении к указаниям результаты решения типовых задач для статически неопределимых стержней.
Методики непосредственного подсчета величин коэффициентов 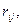
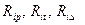 уравнений (4) от силовых воздействий, изменений температурного режима и осадок опор приведены в примерах расчета статически неопределимых рам на соответствующие внешние воздействия.
уравнений (4) от силовых воздействий, изменений температурного режима и осадок опор приведены в примерах расчета статически неопределимых рам на соответствующие внешние воздействия.
ПРИМЕР РАСЧЕТА РАМЫ НА СИЛОВЫЕ ВОЗДЕЙСТВИЯ
Покажем применение алгоритма метода перемещений на примере [6] расчета на внешние силовые воздействия статически неопределимой рамы, показанной на рис. 6 а.
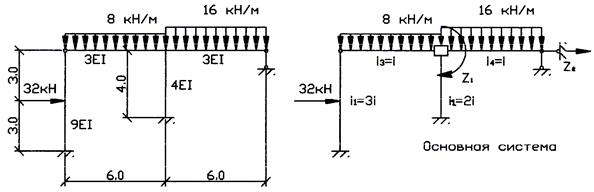
Рис. 6
Данной рама характеризуется степенью статической неопределимости
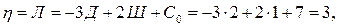
что соответствует трем дополнительным неизвестным по методу сил.
Между тем по методу перемещений число неизвестных, равное степени кинематической неопределимости рамы, составляет лишь
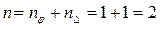 ,
,
что приводит к решению системы двух алгебраических уравнений для нахождения угла поворота среднего жесткого узла рамы 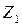 и горизонтального смещения узлов ригеля рамы
и горизонтального смещения узлов ригеля рамы 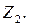
Для образования основной системы метода перемещений в жесткий средний узел рамы ставим угловую связь «шайбу», препятствующую его повороту, и дополняем правый верхний узел рамы линейной связью в виде опорного стерженька, устраняющую линейную подвижность узлов ригеля.
9
Полученная таким образом основная система метода перемещений приведена на рис. 6 б. Неизвестными, число которых совпадает с числом добавленных связей, являются угол поворота среднего жесткого узла рамы 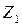 и горизонтальное смещение узлов ригеля рамы
и горизонтальное смещение узлов ригеля рамы 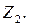
Канонические уравнения метода перемещений, отрицающие наличие реакций в дополнительно введенных связях, при 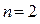 имеют вид:
имеют вид:
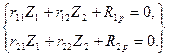 . (7)
. (7)
Для определения величин коэффициентов при неизвестных 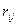 и грузовых слагаемых
и грузовых слагаемых 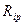 необходимо построить эпюры изгибающих моментов от единичных смещений
необходимо построить эпюры изгибающих моментов от единичных смещений 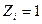 ,
, 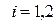 и от внешней силовой нагрузки.
и от внешней силовой нагрузки.
Подсчитываем погонные изгибные жесткости стержней основной системы по формуле (5) и получаем:
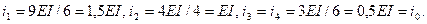
Выражая  через базовую величину
через базовую величину 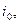 находим
находим 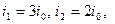

и приводим их значения на основной системе (рис. 6 б).
Деформированное состояние основной системы от единичного угла поворота дополнительной связи «1» приведено на рис. 7 а, где также показана «единичная» эпюра изгибающих моментов 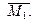 Отметим, что ординаты данной эпюры показаны со стороны растянутых волокон и получены умножением ординат соответствующих эпюр типовых задач из приложения к указаниям на величины
Отметим, что ординаты данной эпюры показаны со стороны растянутых волокон и получены умножением ординат соответствующих эпюр типовых задач из приложения к указаниям на величины 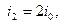
 .
.
Деформированное состояние основной системы от единичного линейного смещения в направлении дополнительной связи «2» приведено на рис. 7 б, на котором также показана «единичная» эпюра изгибающих моментов 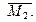 Отметим, что от действия
Отметим, что от действия 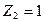 изгибные деформации и изгибающие моменты возникают только на стойках рамы. Ординаты эпюры
изгибные деформации и изгибающие моменты возникают только на стойках рамы. Ординаты эпюры
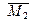 вновь получены умножением ординат соответствующих эпюр типовых задач из приложения к указаниям на величины
вновь получены умножением ординат соответствующих эпюр типовых задач из приложения к указаниям на величины 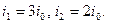
Для определения величины реакции  рассматриваем равновесие узла основной системы с шайбой «1», при этом к частям стержней, примыкающих к «1», прикладываются моменты, взятые с эпюры
рассматриваем равновесие узла основной системы с шайбой «1», при этом к частям стержней, примыкающих к «1», прикладываются моменты, взятые с эпюры  (рис. 7 г). Из условия равенства нулю суммарного момента в шайбе «1» находим:
(рис. 7 г). Из условия равенства нулю суммарного момента в шайбе «1» находим:
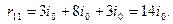
Для определения величины реакции  рассматриваем равновесие узла с шайбой «1», прикладывая к частям стержней, примыкающих к «1», моменты, взятые с эпюры
рассматриваем равновесие узла с шайбой «1», прикладывая к частям стержней, примыкающих к «1», моменты, взятые с эпюры 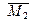 (рис. 7 г). При этом из условия равенства нулю суммарного момента в шайбе «1» находим
(рис. 7 г). При этом из условия равенства нулю суммарного момента в шайбе «1» находим
Рис. 7
В соответствии с теоремой о взаимности реакций, предложенной в 1873 г. Рэлеем и записываемой в виде 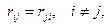 величина реакции
величина реакции
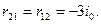
Для определения величины реакции  рассмотрим равновесие отсеченного ригеля, загруженного реакциями, передаваемыми на него стойками. Так как в соответствии с эпюрой
рассмотрим равновесие отсеченного ригеля, загруженного реакциями, передаваемыми на него стойками. Так как в соответствии с эпюрой 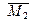 (рис. 7 б) концевые моменты в стойках вращают их против движения часовой стрелки, то опорные реакции в данных стойках создают пары сил, вращающие в противоположную сторону, то есть по движению часовой стрелки.
(рис. 7 б) концевые моменты в стойках вращают их против движения часовой стрелки, то опорные реакции в данных стойках создают пары сил, вращающие в противоположную сторону, то есть по движению часовой стрелки.
Таким образом, ригель передает на стойки в их верхних сечениях силы, действующие направо.
В соответствии с законом Ньютона стойки передают на ригель равные по величине силы, направленные налево и показанные на рис. 7 г. Из условия равновесия отсеченного ригеля находим:
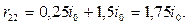
Следует помнить, что величина реакции в дополнительной связи положительна, если ее направление совпадает с выбранным направлением
перемещения 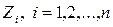 .
.
Грузовая эпюра 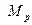 построена в основной системе метода перемещений с использованием типовых задач из приложения к указаниям и приведена на рис. 7 в. Для определения величин грузовых коэффициентов уравнений (7)
построена в основной системе метода перемещений с использованием типовых задач из приложения к указаниям и приведена на рис. 7 в. Для определения величин грузовых коэффициентов уравнений (7) 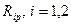 рассматриваем равновесие шайбы «1» и равновесие отсеченного ригеля в соответствии со схемами, приведенными на рис. 7 д.
рассматриваем равновесие шайбы «1» и равновесие отсеченного ригеля в соответствии со схемами, приведенными на рис. 7 д.
При этом из условия равенства нулю суммарного момента в шайбе «1» находим величину 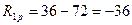 кН м, а из условия равенства нулю суммарной горизонтальной силы, действующей на отсеченный ригель, получаем величину
кН м, а из условия равенства нулю суммарной горизонтальной силы, действующей на отсеченный ригель, получаем величину  кН.
кН.
Изложенный выше способ вычисления величин коэффициентов и грузовых слагаемых канонических уравнений метода перемещений называется статическим. Для проверки полученных значений 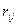 и
и 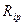 необходимо использовать методику «перемножения» эпюр, заключающуюся в подсчете величин:
необходимо использовать методику «перемножения» эпюр, заключающуюся в подсчете величин:
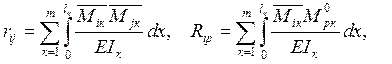 (8)
(8)
где 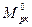 - эпюра изгибающих моментов от внешней нагрузки в произвольной геометрически неизменяемой и статически определимой системе, получаемой из исходной системы устранением всех «лишних» связей и не содержащей дополнительных связей основной системы метода перемещений.
- эпюра изгибающих моментов от внешней нагрузки в произвольной геометрически неизменяемой и статически определимой системе, получаемой из исходной системы устранением всех «лишних» связей и не содержащей дополнительных связей основной системы метода перемещений.
Отметим, что вычисление величин определенных интегралов (8) можно осуществить по формуле Симпсона или по способу Верещагина.
Изложенная методика подсчета величин 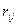 и
и 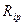 уравнений (4) позволяет проверить значения
уравнений (4) позволяет проверить значения 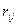 и
и 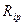 , полученные статическим способом.
, полученные статическим способом.
Для рассматриваемого примера система канонических уравнений (7) после подстановки вычисленных значений 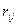 и
и 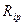 принимает вид:
принимает вид:
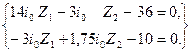 .
.
12
Решая данную систему уравнений, находим величины перемещений:
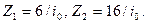
Для построения расчетной эпюры изгибающих моментов в раме необходимо промасштабировать единичные эпюры моментов, умножив их на
вычисленные величины узловых перемещений, и сложить их с эпюрой грузовых моментов 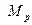 , то есть использовать формулу:
, то есть использовать формулу:
 (9)
(9)
принимающую в случае рассматриваемого примера с n = 2 вид:
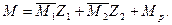
Построенная по данной формуле расчетная эпюра изгибающих моментов  приведена на рис. 8 а.
приведена на рис. 8 а.
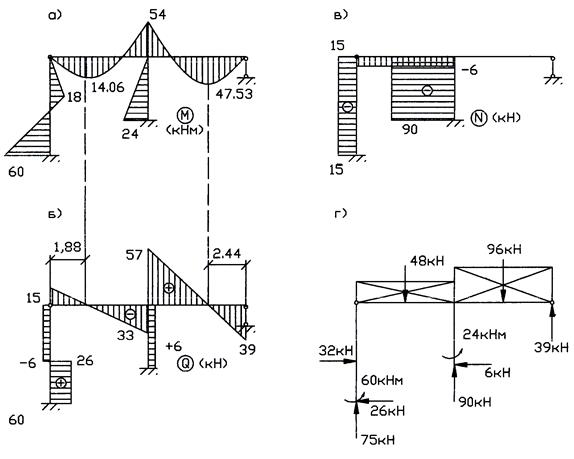
Рис. 8
По методике, аналогичной используемой в методе сил, по расчетной эпюре изгибающих моментов M строится расчетная эпюра поперечных (перерезывающих) сил Q (рис. 8 б), а затем с использованием ординат эпюры Q строится расчетная эпюра продольных сил N (рис. 8 в).
13
Для проверки правильности построения расчетных эпюр M, Q, N необходимо:
1) рассмотреть поочередно все узлы рамы и удостовериться в выполне-
нии для них уравнений равновесия:
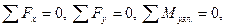
2) провести статическую проверку равновесия рамы: освободить раму
от опорных закреплений, заменив их реакциями опорных связей, и проверить условия равновесия всей рамы с учетом внешней нагрузки (рис. 8 г):
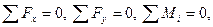
3) провести кинематическую проверку расчетной эпюры M, заклю-
чающуюся в выполнении условия:
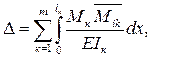 (10)
(10)
где 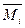 - эпюра моментов, построенная в любой основной системе метода сил от совместного действия «единичных» усилий
- эпюра моментов, построенная в любой основной системе метода сил от совместного действия «единичных» усилий 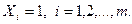
Для рассматриваемой рамы эпюра 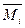 приведена на рис. 9, величина определенного интеграла в формуле (10) может быть подсчитана по формуле Симпсона или по способу Верещагина.
приведена на рис. 9, величина определенного интеграла в формуле (10) может быть подсчитана по формуле Симпсона или по способу Верещагина.
Рис. 9
Выполнение всех перечисленных проверок расчетных эпюр M, Q, N свидетельствует о правильности расчета статически неопределимой рамы методом перемещений на действие внешних силовых нагрузок. На основании расчетных эпюр M, Q, N проверяется прочность характерных сечений рамы и определяются величины характерных перемещений в раме.
ПРИМЕР РАСЧЕТА РАМЫ
НА ИЗМЕНЕНИЯ ТЕМПЕРАТУРНОГО РЕЖИМА
Наряду с внешними силовыми воздействиями статически неопределимые рамы подвергаются также изменениям температурного режима, причем возникающие при этом напряжения зачастую сопоставимы с напряжениями от внешних нагрузок.
Покажем применение алгоритма метода перемещений на примере [4] расчета на изменения температурного режима статически неопределимой рамы, показанной на рис. 10 а.

Рис. 10
Данной рама характеризуется степенью статической неопределимости
что соответствует пяти дополнительным неизвестным по методу сил.
Между тем по методу перемещений число неизвестных, равное степени кинематической неопределимости рамы, составляет лишь
 ,
,
что приводит к решению системы двух алгебраических уравнений для нахождения угла поворота среднего жесткого узла рамы  и правого жесткого узла рамы
и правого жесткого узла рамы 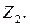
Для образования основной системы метода перемещений в жесткие средний и правый узлы рамы ставим угловые связи «шайбы», препятствующие их повороту. Полученная таким образом основная система метода перемещений приведена на рис. 10 б.
Канонические уравнения метода перемещений при расчете рамных систем на действия температуры имеют вид:
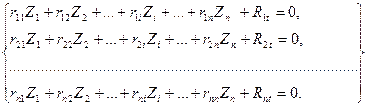 . (11)
. (11)
Коэффициенты при неизвестных  вычисляются так же, как и при действии внешней нагрузки. Для определения реакций в дополнительных связях основной системы от температурных воздействий
вычисляются так же, как и при действии внешней нагрузки. Для определения реакций в дополнительных связях основной системы от температурных воздействий 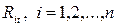 используем результаты решения типовых задач для статически неопределимых стержней, подвергнутых неравномерному нагреву, которые приведены в приложении к методическим указаниям.
используем результаты решения типовых задач для статически неопределимых стержней, подвергнутых неравномерному нагреву, которые приведены в приложении к методическим указаниям.
Для рамы (рис. 10 а) принимаем внутреннюю и внешнюю температуры равными 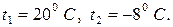 Длины всех стержней равны
Длины всех стержней равны 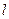 , постоянны изгибные жесткости стержней
, постоянны изгибные жесткости стержней 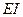 и погонные изгибные жесткости
и погонные изгибные жесткости 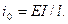 Принимаем также высоту для всех стержней рамы равной
Принимаем также высоту для всех стержней рамы равной 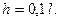
Считаем в дальнейшем, что температура линейно изменяется по высоте сечения  от величины
от величины 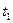 до величины
до величины 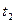 . Кроме того, представляем температурное воздействие на каждый стержень рамы в виде суммы симметричного равномерного нагрева средней температурой
. Кроме того, представляем температурное воздействие на каждый стержень рамы в виде суммы симметричного равномерного нагрева средней температурой 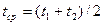 , вызывающего удлинение стержня на величину
, вызывающего удлинение стержня на величину 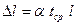 , и кососимметричного действия температурного перепада величиной
, и кососимметричного действия температурного перепада величиной 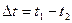 , при котором искривляется ось стержня при сохранении его длины.
, при котором искривляется ось стержня при сохранении его длины.
Для стержней рамы из рассматриваемого примера (рис. 10 а) величины средних температур и температурных перепадов будут равны:
1) для обоих ригелей 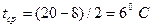 ,
, 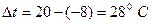 ,
,
2) для левой стойки  ,
, 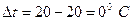 ,
,
3) для правой стойки 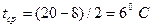 ,
, 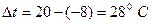 .
.
Весьма ответственным этапом расчета на температурные воздействия является построение эпюры изгибающих моментов от температуры 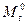 в основной системе метода перемещений. Для упрощения данной задачи выполняем ее в два этапа. На первом из них не учитываем удлинений стержней от средней температуры и строим частную эпюру от неравномерного нагрева
в основной системе метода перемещений. Для упрощения данной задачи выполняем ее в два этапа. На первом из них не учитываем удлинений стержней от средней температуры и строим частную эпюру от неравномерного нагрева 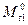 . На втором этапе учитываем лишь удлинения стержней от средней температуры и строим частную эпюру от равномерного нагрева
. На втором этапе учитываем лишь удлинения стержней от средней температуры и строим частную эпюру от равномерного нагрева 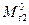 .
.
Эпюру 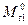 (рис. 10 д) необходимо строить последовательно для каждого стержня основной системы (рис. 10 б), привлекая для этого результаты решения типовых задач, приведенные в приложении к указаниям.
(рис. 10 д) необходимо строить последовательно для каждого стержня основной системы (рис. 10 б), привлекая для этого результаты решения типовых задач, приведенные в приложении к указаниям.
Например, для ригелей рамы и ее правой стойки разность температур одинакова и равна 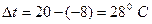 . По табл. 1 приложения для стержня, жестко защемленного по двум концам, эпюра
. По табл. 1 приложения для стержня, жестко защемленного по двум концам, эпюра 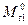 имеет вид прямоугольника с ординатой:
имеет вид прямоугольника с ординатой:
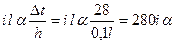 .
.
Так как для левой стойки рамы 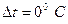 , то эпюра
, то эпюра  для нее отсутствует.
для нее отсутствует.
Для построения эпюры  (рис. 10 е) от равномерного нагрева необходим учет относительного смещения концов всех стержней основной системы. При отдельном рассмотрении каждого стержня с использованием нумерации узлов с рис. 10 а устанавливаем следующее:
(рис. 10 е) от равномерного нагрева необходим учет относительного смещения концов всех стержней основной системы. При отдельном рассмотрении каждого стержня с использованием нумерации узлов с рис. 10 а устанавливаем следующее:
1) для стержня 0-1 правая заделка смещается вверх на величину уд-
линения стойки 1-3 от действия 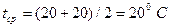 , равного
, равного 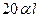 . В соответствии с табл. 1 приложения к указаниям при единичном взаимном смещении концов моменты равны
. В соответствии с табл. 1 приложения к указаниям при единичном взаимном смещении концов моменты равны 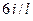 , а от смещения, равного
, а от смещения, равного 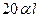 , моменты составят
, моменты составят 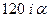 ,
,
2) для стержня 1-2 левая стойка удлиняется на величину 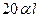 , пра-
, пра-
вая– удлиняется на величину 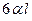 , поэтому относительное смещение концов стержня 1-2 составит
, поэтому относительное смещение концов стержня 1-2 составит  . В этой связи моменты на концах стержня равны
. В этой связи моменты на концах стержня равны 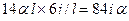 ,
,
3) для стержня 1-3 верхний узел сместится вправо на величину удли-
нения ригеля 0-1, равного 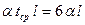 . При единичном смещении заделки для стержня с шарниром на другом конце момент равен
. При единичном смещении заделки для стержня с шарниром на другом конце момент равен 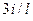 , тогда от смещения
, тогда от смещения  момент составит
момент составит 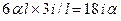 ,
,
4) для стержня 2-4 смещение верхнего узла равняется сумме удлине-
ний стержней 0-1 и 1-2 от действия средней температуры 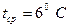 , поэтому моменты на концах стойки 2-4 составят
, поэтому моменты на концах стойки 2-4 составят 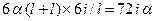 .
.
Суммируя ординаты эпюр от неравномерного нагрева 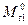 и равномерного нагрева
и равномерного нагрева 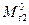
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|