
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 1. Пример 5. Пример 6. Пример 8. Пример 9. Пример 10.
В заключение для Н.И. хотелось бы отметить.
Ранее мы ввели понятие элементарной функции и установили, что производная 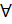 -й элементарной функции представляет так же элементарную функцию. Установили, что операция дифференцирования не выводит нас из класса элементарных функций.
-й элементарной функции представляет так же элементарную функцию. Установили, что операция дифференцирования не выводит нас из класса элементарных функций.
Отметим, что с операции интегрирования дело обстоит иначе. Можно доказать, что интегралы от некоторых элементарных функций уже не являются элементарными.
Примерами таких интегралов могут служить следующие:
1. 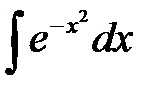 - интеграл Пуассона
- интеграл Пуассона
2. 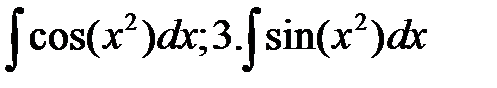 -интегралы Френеля
-интегралы Френеля
4. 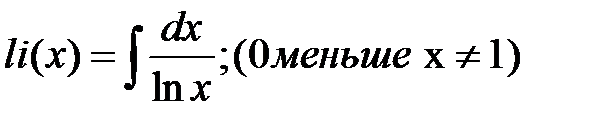 -интегральный логарифм
-интегральный логарифм
5. 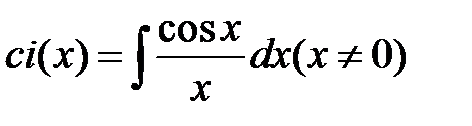
6. 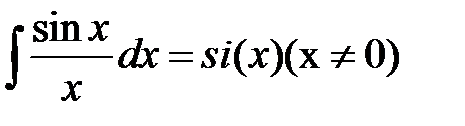 -интегральный синус .
-интегральный синус .
7. 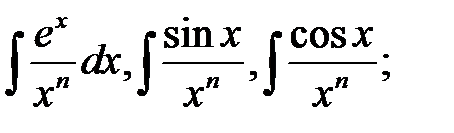
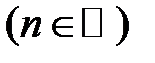 и многие другие .
и многие другие .
Каждый из указанных интегралов представляет собой функцию не являющуюся элементарной.
Эти функции реально  -ют и играют важную роль в различных вопросах физики.
-ют и играют важную роль в различных вопросах физики.
1-я называется интегралом Пуассона или интегралом ошибок. Используют в статической физике, в теории теплопроводности иди диффузии.
2^3.-интегралы Френеля- используются в оптике. Не вычисляются в элементарных функциях
Пример 1
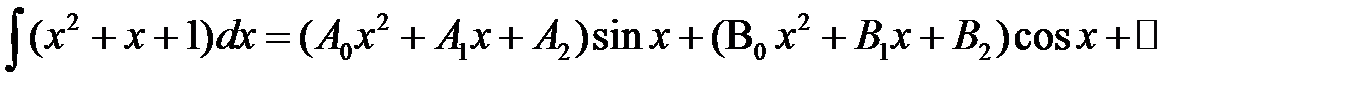
Решение:
Дифференцируем обе части равенства и получаем:
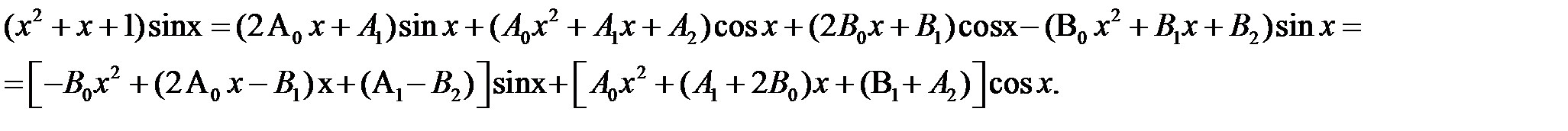
Приравниваем коэффициенты при одинаковых слагаемых, получаем систему уравнений
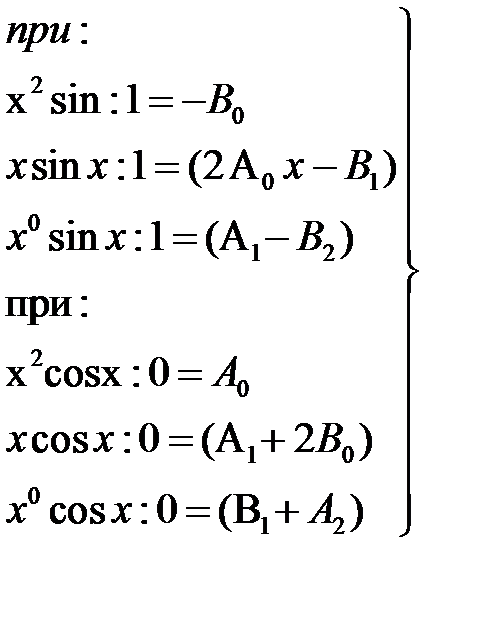
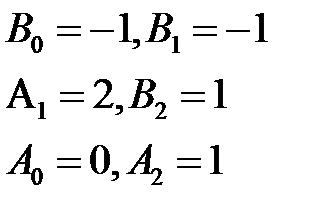
Тогда- 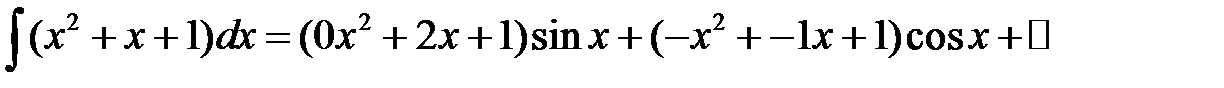
Проверка:
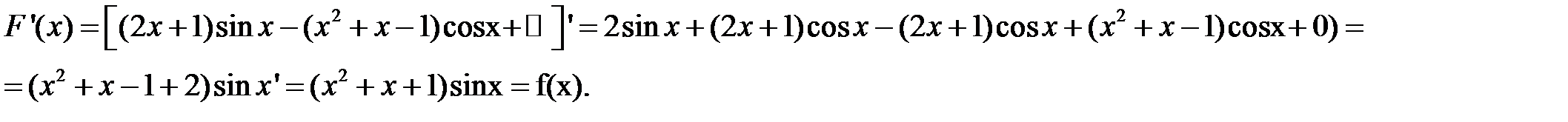
Пример 2
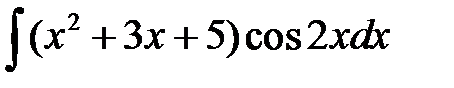
Полагаем 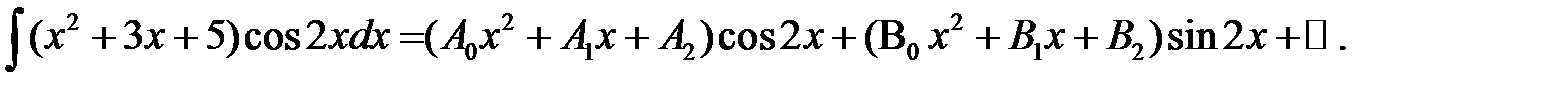
Дифференцируя получим:
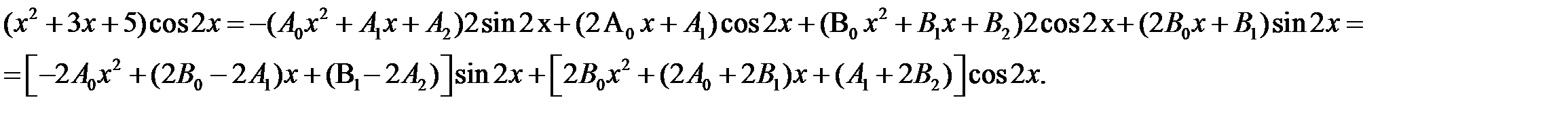
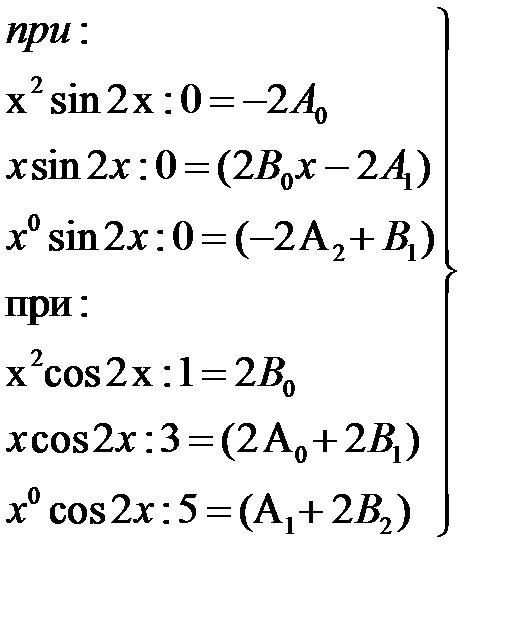
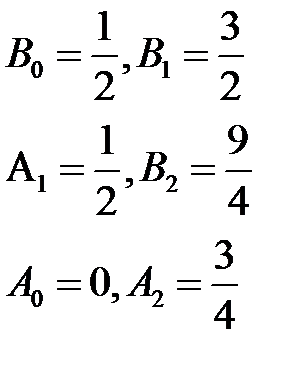
Тогда-
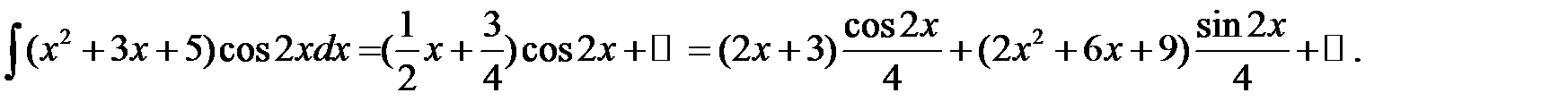
Проверка:
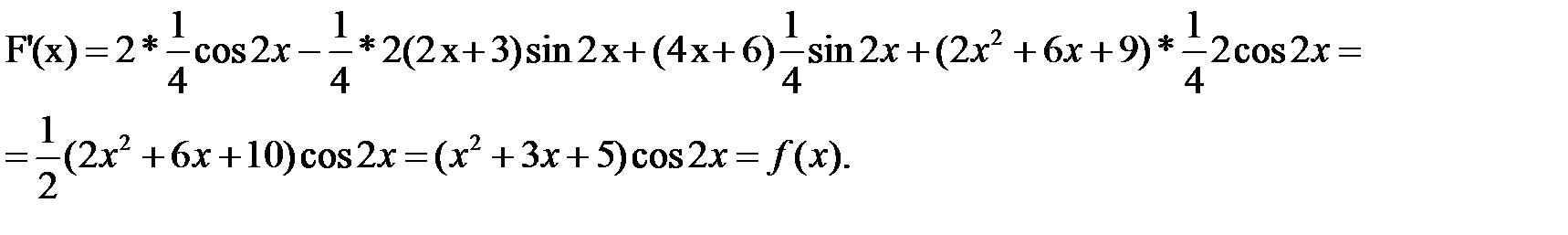
Пример 3 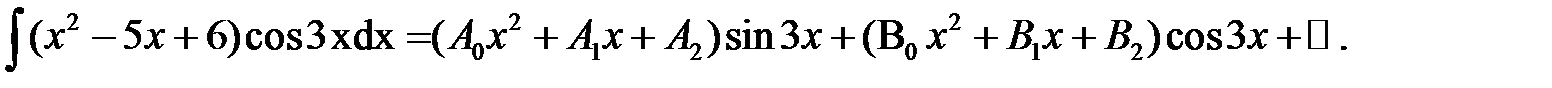
Дифференцируя получим:
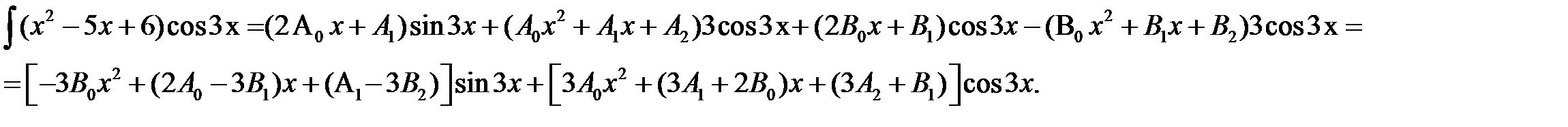
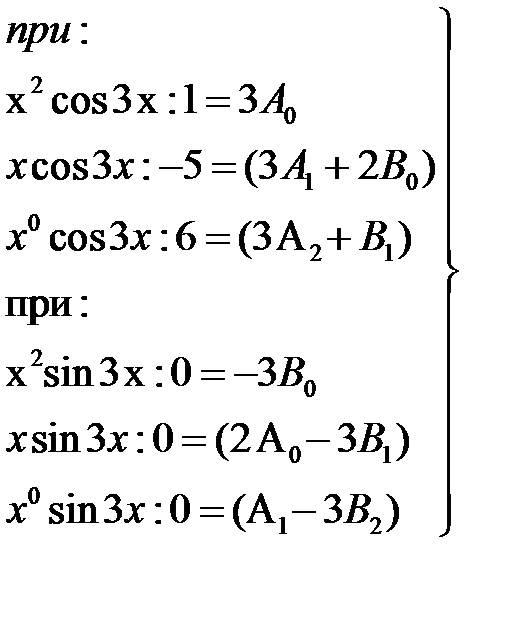
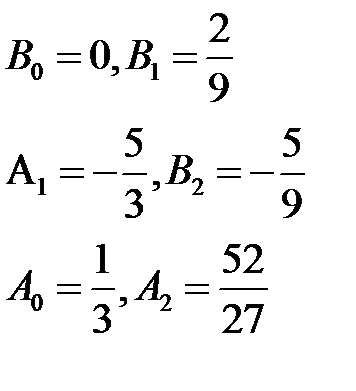
Тогда-
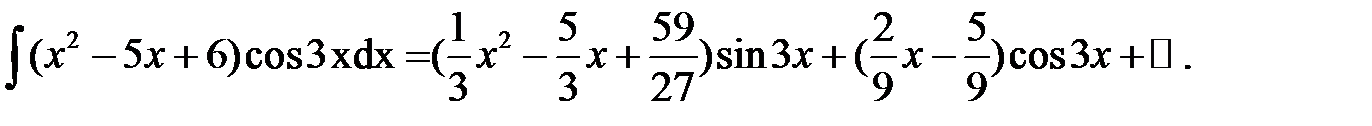
Проверка:
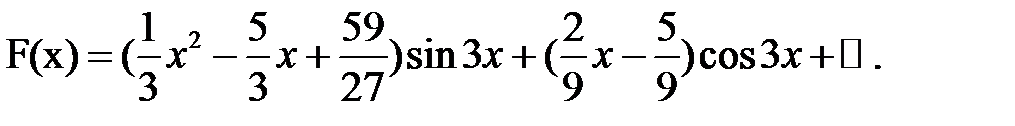
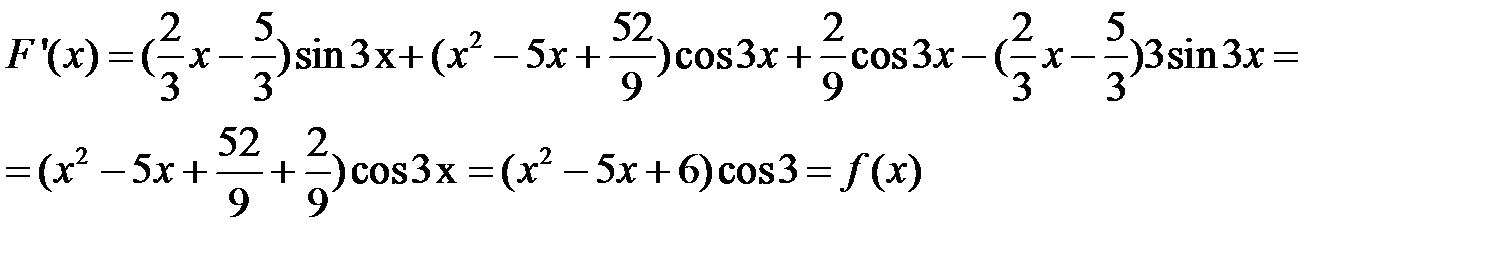
Пример 4 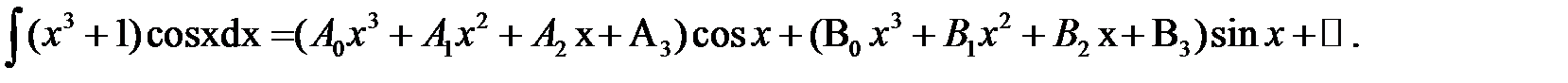
Решение:
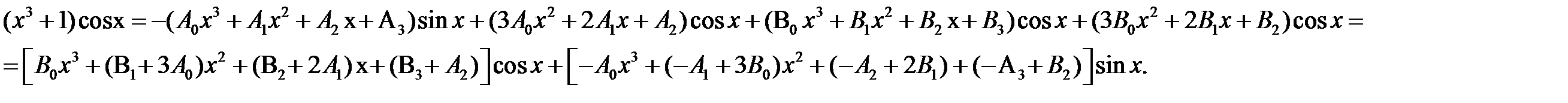
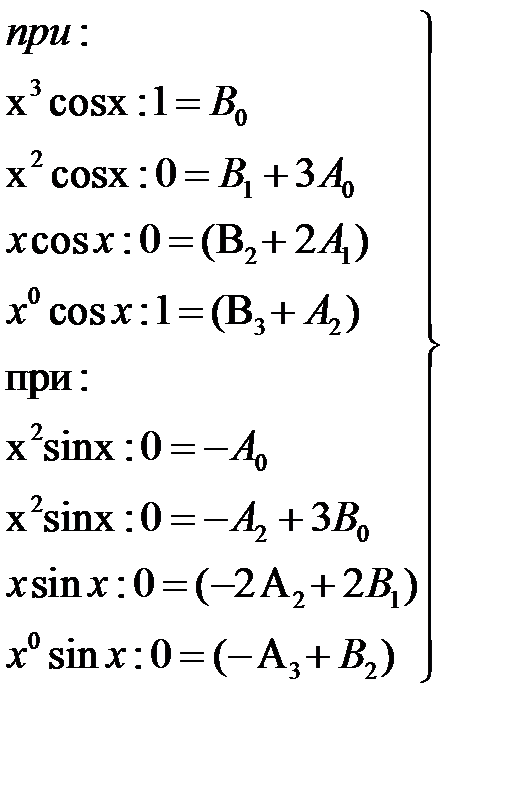
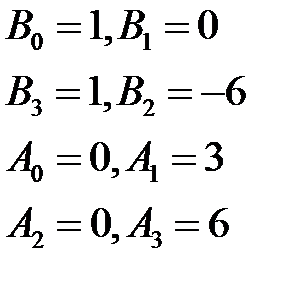
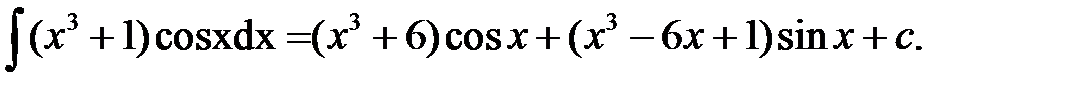
Пример 5
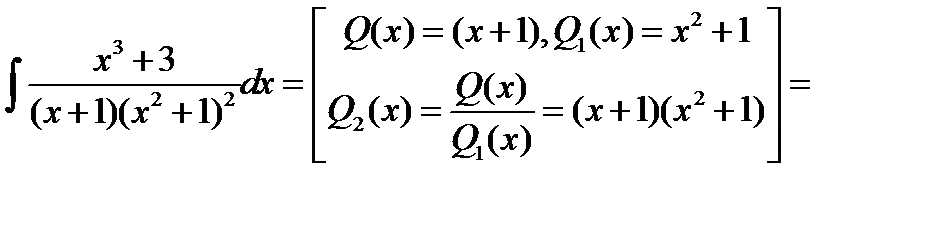
(1)
( 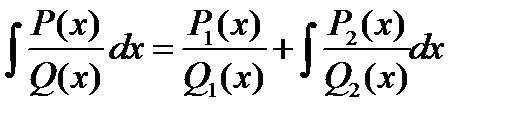
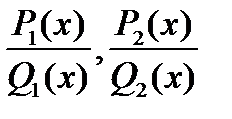 - Правильные дроби, степени числителей меньше на 1 знаменателя.)
- Правильные дроби, степени числителей меньше на 1 знаменателя.)
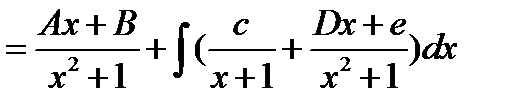
( (1) дифференцируем и получим в равносильной форме 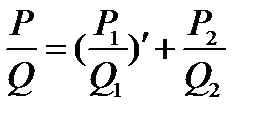 ).
).
Т.е.
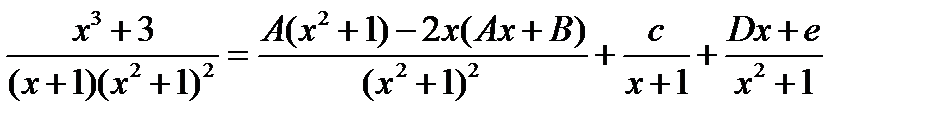
Приводим к общему знаменателю дроби и приравниваем числители.
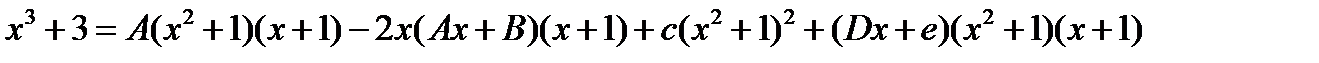
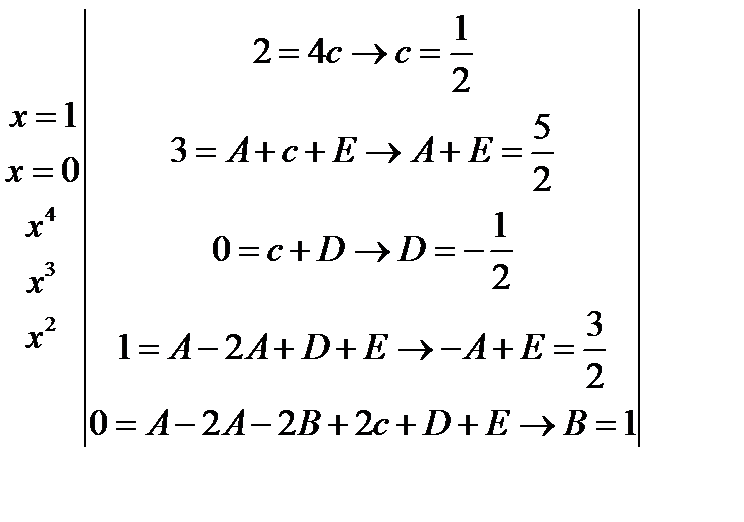
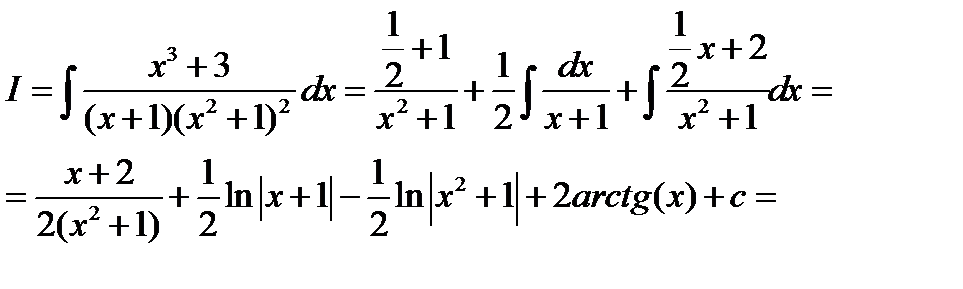
Тогда
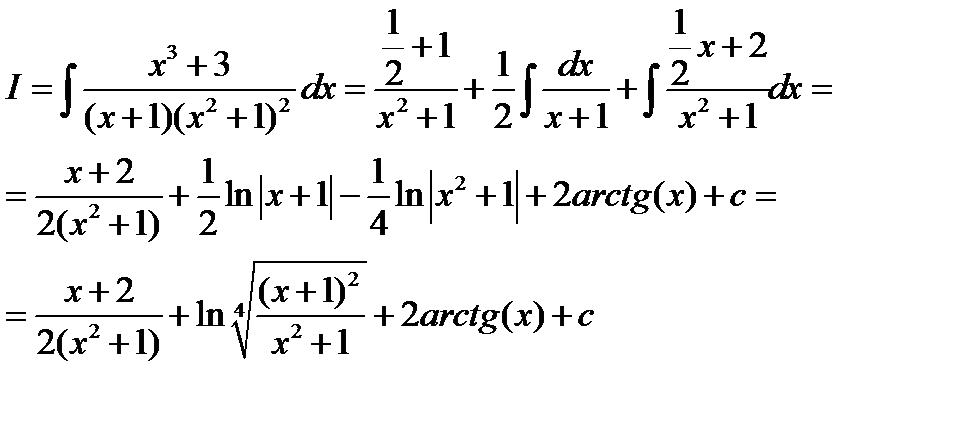
Пример 6
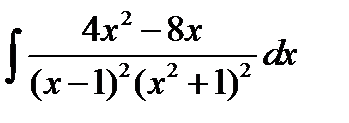
Этот интеграл можно вычислить двумя способами.
А)
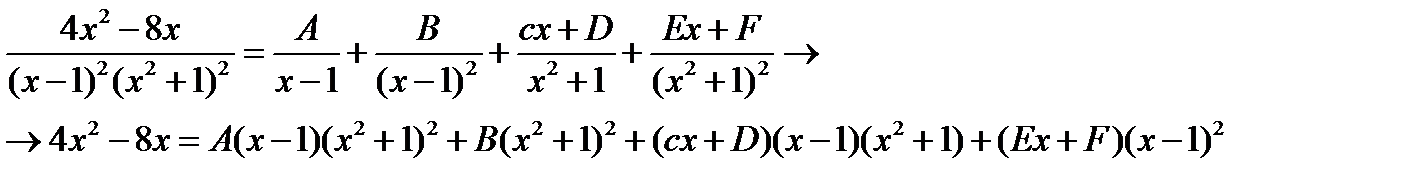
А далее известно, можно получить шесть уравнений с шестью неизвестными A,B,C,D,E,F.
В)
Найдем этот интеграл методом Остроградского.
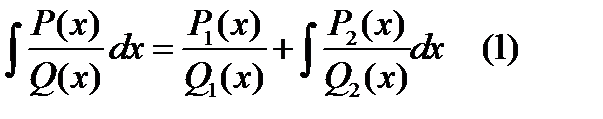
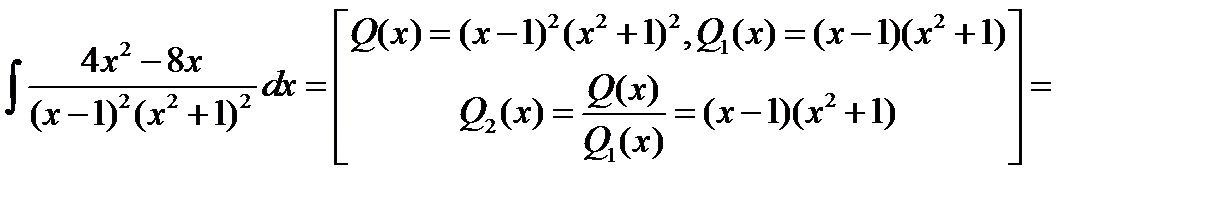
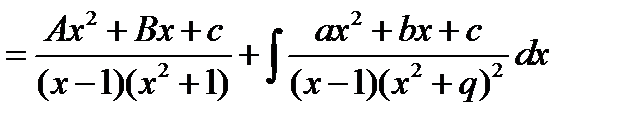
Рациональную дробь 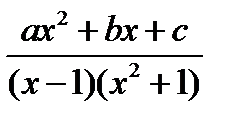 удобно представить в виде суммы элементарных дробей.
удобно представить в виде суммы элементарных дробей.
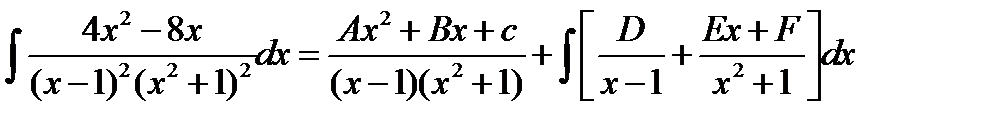
Дифференцируем обе части этого равенства, получаем:
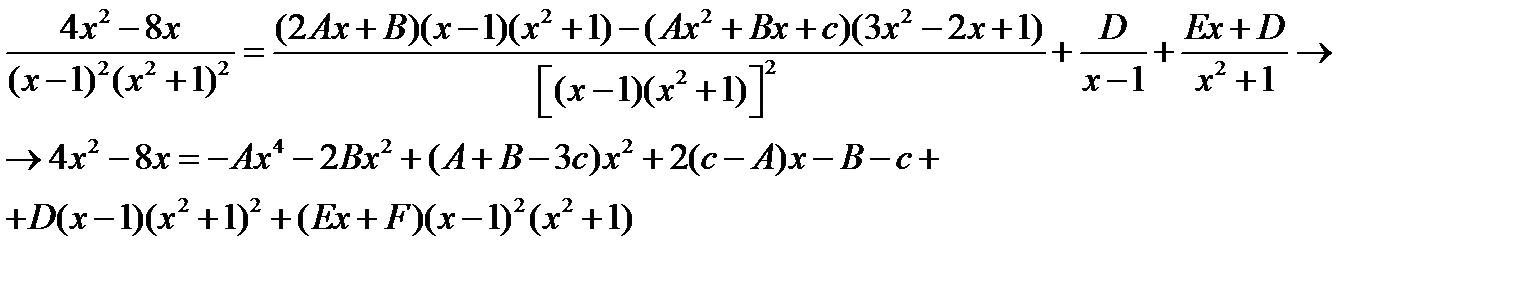
Приравнивая коэффициенты при одинаковых степенях буквы x, получаем систему
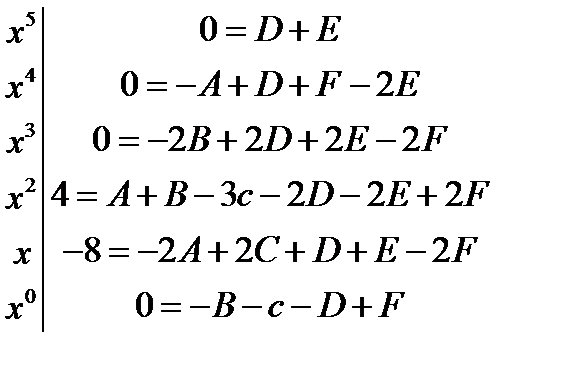
Решая эту систему находим
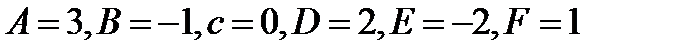
Итак
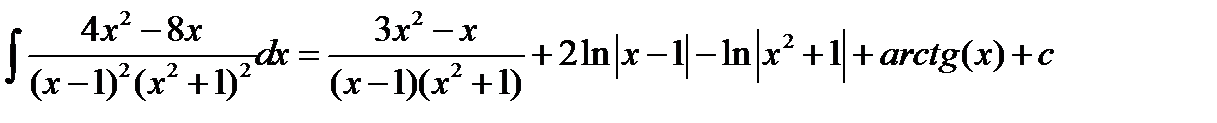
Описанные выше методы интегрирования рациональных функций хотя и обладают общностью, так как в отдельных случаях рассматриваемые интеграл от рассматриваемой функции может быть значительно проще вычислен с помощью метода замены переменных или непосредственно с помощью тех или иных искусственных приемов.
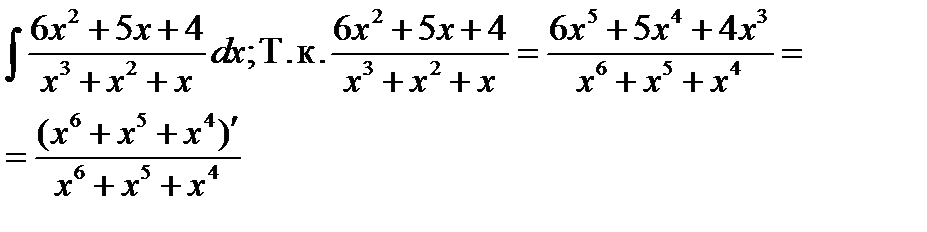
Заметим, что
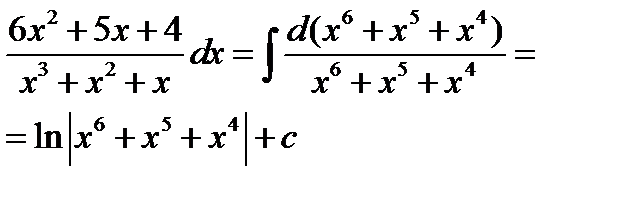
Пример 8
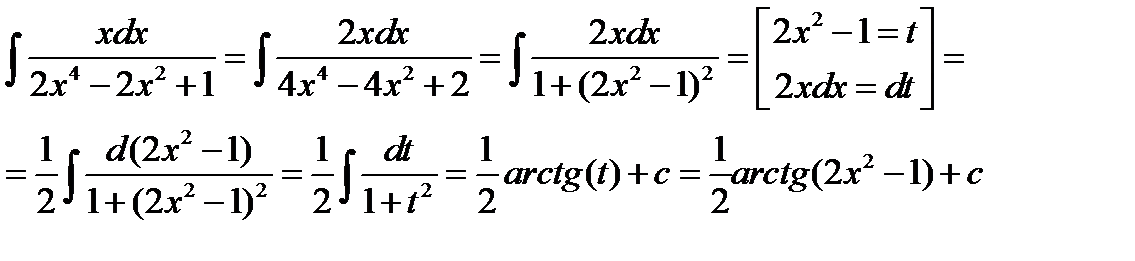
Пример 9
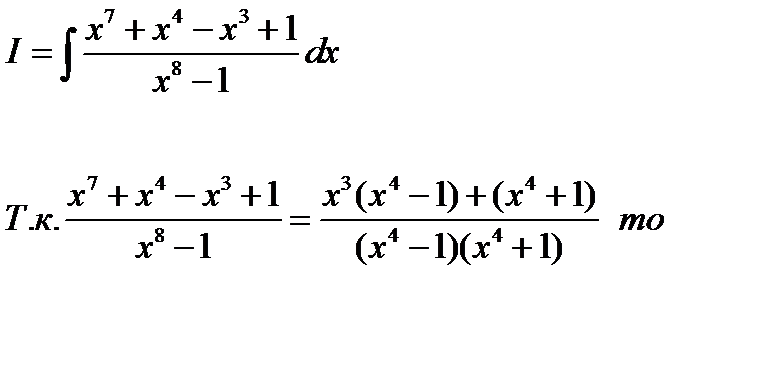
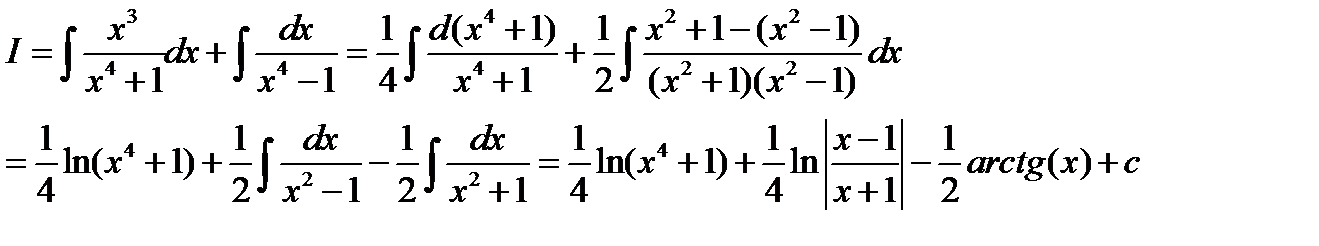
Как видно, вычисления были не сложными, разложение подынтегральной дроби на элементарные было бы здесь весьма громоздким и привело бы непосредственно к усложнению формы ответа.
Обратимся к интегралу вида В)
В) 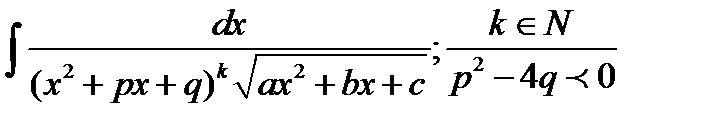
Если 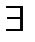 число
число 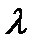 такое, что для всех х
такое, что для всех х 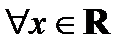 выполняется равенство
выполняется равенство
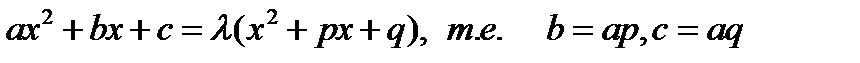 , то интеграл в) можно представить в виде линейной комбинации интегралов
, то интеграл в) можно представить в виде линейной комбинации интегралов
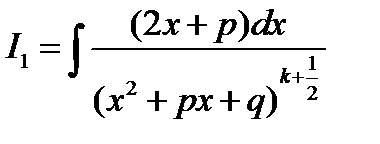 и
и 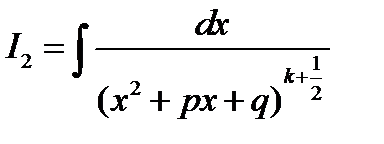
Интеграл I1 – сводится к табличному, а для I2 применяем подстановку Абеля.
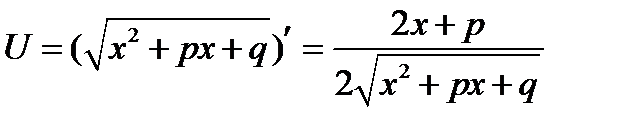 которая сведет его к интегралу от многочлена.
которая сведет его к интегралу от многочлена.
Если 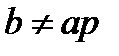 , то используется подстановка
, то используется подстановка 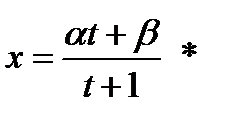
Где 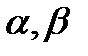 подбираются такими, чтобы коэффициенты при t в квадратных трехчленах подынтегральной функции обратились в нуль. При этом интегралы принимают вид:
подбираются такими, чтобы коэффициенты при t в квадратных трехчленах подынтегральной функции обратились в нуль. При этом интегралы принимают вид:
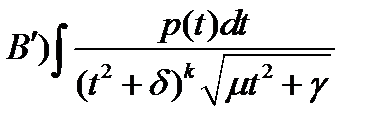 , гдеP(t) – огочлен степени 2k-1,
, гдеP(t) – огочлен степени 2k-1, 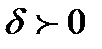
Если b=ap, но 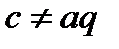 (случай b=ap и c=aq – рассмотрен выше)
(случай b=ap и c=aq – рассмотрен выше)
То вместо подстановки (*) можно применить подстановку 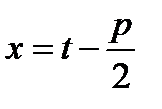 .
.
Чтобы вычислить интеграл 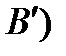 разложим правильную рациональную дробь на простые дроби и представим
разложим правильную рациональную дробь на простые дроби и представим  в виде линейной комбинации интегралов вида
в виде линейной комбинации интегралов вида
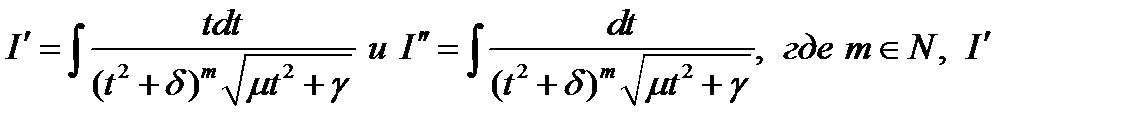
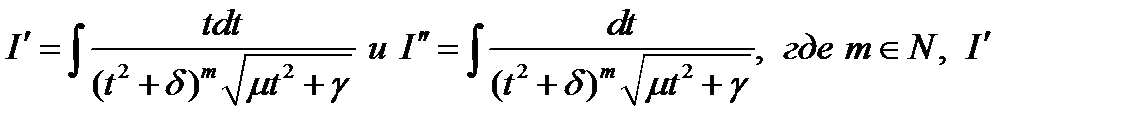 вычисляется с помощью подстановки
вычисляется с помощью подстановки 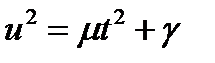 , а
, а 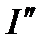 - с помощью подстановки Абеля
- с помощью подстановки Абеля 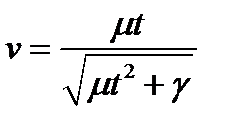
Обратились в нуль. При этом интеграл в) принимает вид
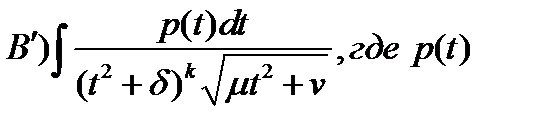 - многочлен степени «2k-1»,
- многочлен степени «2k-1», 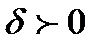 .
.
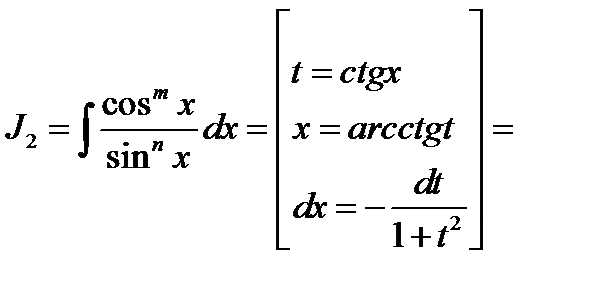
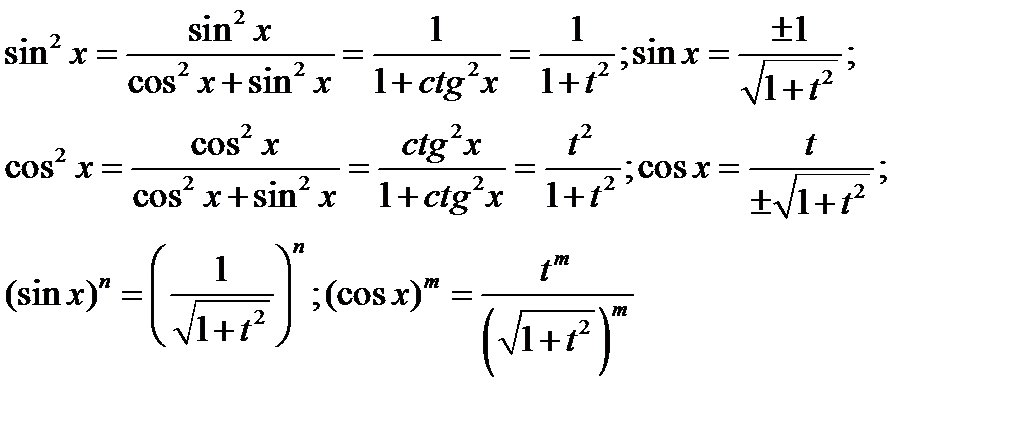
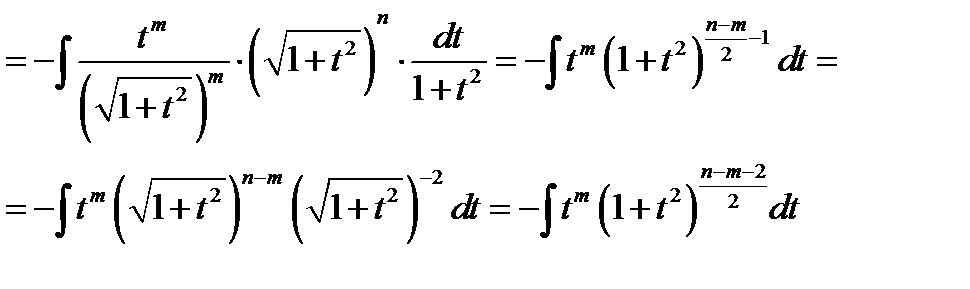
Пример 10.
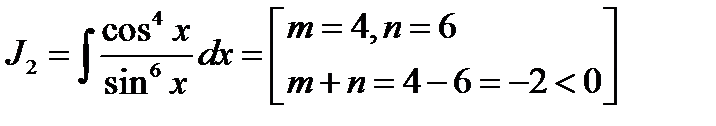
Т.к. в числителе находится степень cosx, то удобной подстановкой является
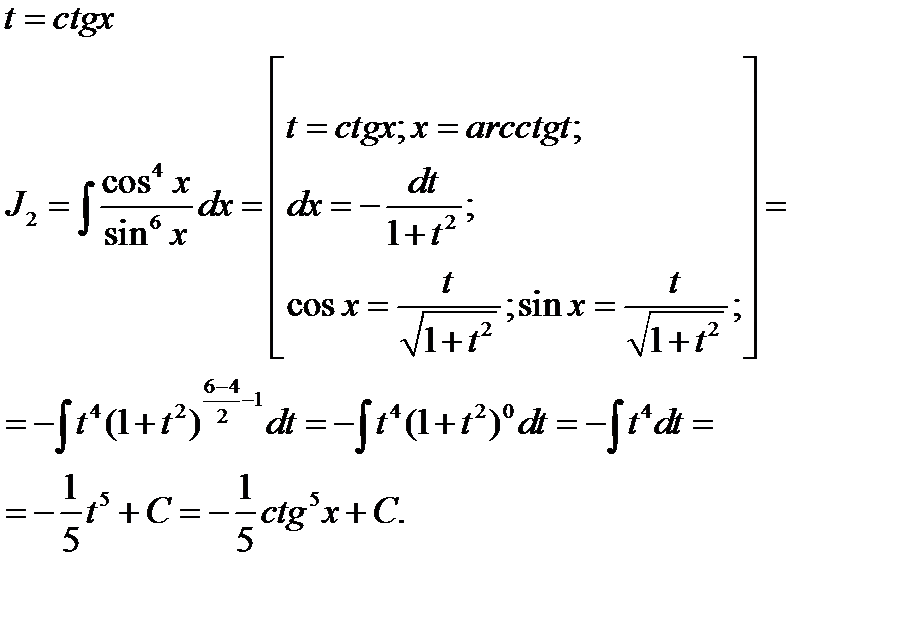
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|