
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока
Преподаватель - Брыкало А.А.
brukalo_aa@mail.ru
https://vk.com/id399759339
Конспект урока «Математика»
Дата08.06.2020
Группа87профессия«Машинист крана (крановщик)» курс2
Тема 138:Практическое занятие №73 «Векторы в пространстве»
Форма работы:индивидуальная, электронное обучение
Тип урока:урок совершенствования знаний, умений и навыков
Продолжительность урока: 1 час
Цель урока:корректировать знания, умения и навыки по теме «Векторы в пространстве», закрепить и систематизировать знания по данной теме.
Используемая литература:
Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г
Интернет-ресурсы:
Методика преподавания математики http://methmath.chat.ru/
Ход урока
Организационный этап:
Мотивационный модуль
Ребята, на этом уроке вы повторите материал по теме «Векторы в пространстве», выполните практическую работу.
Основная часть:
Объясняющий модуль
Теоретический материал для самостоятельного изучения
1. Повторите теоретический материал.
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом  или
или 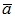 . Вектор
. Вектор 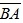 называется противоположным вектору
называется противоположным вектору  и может быть обозначен
и может быть обозначен 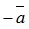 .
.
Сформулируем ряд базовых определений.
Длиной или модулем вектора  называется длина отрезка и обозначается
называется длина отрезка и обозначается 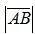 . Вектор нулевой длины (его суть - точка) называется нулевым
. Вектор нулевой длины (его суть - точка) называется нулевым 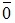 и направления не имеет. Вектор
и направления не имеет. Вектор  единичной длины, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора
единичной длины, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора 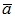 , называется ортом вектора
, называется ортом вектора 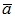 .
.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, записывают  . Коллинеарные векторы могут иметь совпадающие или противоположные направления. Нулевой вектор считают коллинеарным любому вектору.
. Коллинеарные векторы могут иметь совпадающие или противоположные направления. Нулевой вектор считают коллинеарным любому вектору.
Векторы называются равными 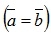 , если они коллинеарны, одинаково направлены и имеют одинаковые длины.
, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Рассмотрим в пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и обозначим их через 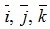 соответственно. Выберем произвольный вектор пространства и совместим его начало с началом координат. Спроектируем вектор на координатные оси и обозначим проекции через ax, ay, az соответственно. Тогда нетрудно показать, что
соответственно. Выберем произвольный вектор пространства и совместим его начало с началом координат. Спроектируем вектор на координатные оси и обозначим проекции через ax, ay, az соответственно. Тогда нетрудно показать, что
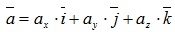 .
.
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.
Числа ax, ay, az называются координатами вектора 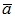 . Таким образом, координаты вектора являются его проекциями на оси координат. Векторное равенство часто записывают в виде
. Таким образом, координаты вектора являются его проекциями на оси координат. Векторное равенство часто записывают в виде
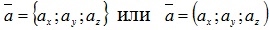 .
.
Мы будем использовать обозначение вектора в фигурных скобках, чтобы визуально легче различать координаты вектора и координаты точки. С использованием формулы длины отрезка, известной из школьной геометрии, можно найти выражение для вычисления модуля вектора :
 ,
,
то есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора 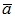 направляющими, и для них выполняется соотношение:
направляющими, и для них выполняется соотношение: 
Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.
Пусть в трехмерном пространстве заданы векторы 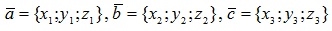 своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).
своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то есть если
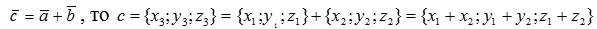 .
.
Данная формула имеет место для произвольного конечного числа слагаемых.
Геометрически два вектора складываются по двум правилам:
а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;
б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.
2. Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если 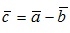 , то
, то
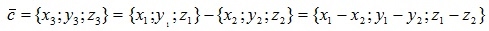 .
.
Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координат его конца вычесть координаты его начала. Действительно, любой вектор пространства  может быть представлен в виде разности двух векторов, исходящих из начала координат:
может быть представлен в виде разности двух векторов, исходящих из начала координат: 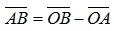 . Координаты векторов
. Координаты векторов 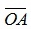 и
и 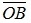 совпадают с координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.
совпадают с координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:  .
.
При λ>0 – вектор 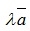 сонаправлен
сонаправлен 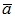 ; λ<0 – вектор
; λ<0 – вектор 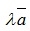 противоположно направлен
противоположно направлен 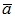 ; |λ|>1 – длина вектора
; |λ|>1 – длина вектора 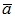 увеличивается в λ раз; |λ|<1 – длина вектора
увеличивается в λ раз; |λ|<1 – длина вектора 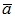 уменьшается в λ раз.
уменьшается в λ раз.
4. Пусть в пространстве задана направленная прямая (ось l), вектор 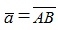 задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A’ и B’.
задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A’ и B’.
Проекцией 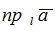 вектора
вектора 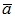 на ось l называется длина вектора
на ось l называется длина вектора  , взятая со знаком «+», если вектор
, взятая со знаком «+», если вектор  и ось l сонаправлены, и со знаком «–», если
и ось l сонаправлены, и со знаком «–», если  и l противоположно направлены.
и l противоположно направлены.
Если в качестве оси l взять некоторый другой вектор 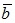 , то получим проекцию вектора
, то получим проекцию вектора 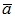 на вектор
на вектор 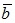 .
.
Рассмотрим некоторые основные свойства проекций:
1) проекция вектора 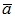 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 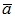 на косинус угла между вектором и осью, то есть
на косинус угла между вектором и осью, то есть 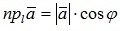 ;
;
2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;
3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.
5. Скалярным произведением  векторов
векторов 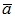 и
и 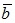 называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть
называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть
 .
.
Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол  , поэтому его косинус равен 1.
, поэтому его косинус равен 1.
Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения 
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 
Теорема 2.3. Скалярное произведение двух векторов 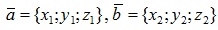 , заданных своими координатами, равно сумме произведений их одноименных координат, то есть
, заданных своими координатами, равно сумме произведений их одноименных координат, то есть
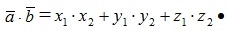
С помощью скалярного произведения векторов можно вычислить угол между ними. Если заданы два ненулевых вектора своими координатами
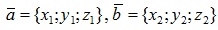 , то косинус угла φ между ними:
, то косинус угла φ между ними:
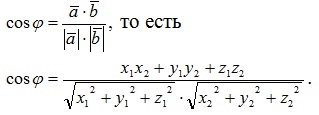
Отсюда следует условие перпендикулярности ненулевых векторов 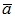 и
и 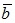 :
:

Нахождение проекции вектора 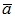 на направление, заданное вектором
на направление, заданное вектором 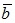 , может осуществляться по формуле
, может осуществляться по формуле
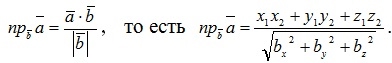
2. Решение задач
Пример 1. С помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
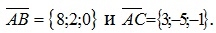
Решение:
Вычислим модули векторов и их скалярное произведение:
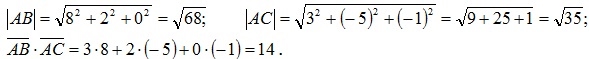
Отсюда получим косинус искомого угла

Выполнение практической части работы
2.Оформление работы:
Практическое занятие № 73
Тема: «Векторы в пространстве»
Цель: корректировать знания, умения и навыки по теме «Векторы в пространстве», закрепить и систематизировать знания по данной теме.
Практическая часть работы:
1. В прямоугольном треугольнике 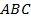 катеты
катеты 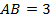 ,
, 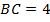
Вычислить:
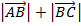

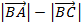
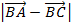
2. Доказать неравенство: 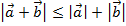
3. Доказать, что сумма любого набора векторов, для которых конец одного совпадает с началом следующего, равна вектору, соединяющему начало первого вектора и конец последнего:
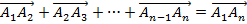
Домашнее задание:
Оформить отчет по практической работе
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|