
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры оформления решения заданий письменного экзамена по математике (профильный уровень)
Примеры оформления решения заданий письменного экзамена по математике (профильный уровень)
Задание №1
Вариант 81
№1
Решение.
На всей области определения убывает функция 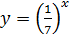 .
.
Ответ: в.
Вариант 87
№1
Решение.
Из перечисленных функций степенной является функция 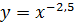 .
.
Ответ: в.
Вариант 95
№1
Решение.
Уравнения, не имеющие корней:  .
.
Ответ: в, г.
Вариант 103
№1
Решение.
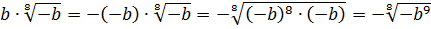 .
.
Ответ: г.
Вариант 109
№1
Решение.
Графической иллюстрацией системы уравнений  является рисунок в.
является рисунок в.
Ответ: в.
Задание №2
Вариант 84
№2
Решение.
При вращении прямоугольника около одной из сторон получается цилиндр.
Ответ: а.
Вариант 90
№2
Решение.
Из перечисленных утверждений верным является утверждение: треугольник DA1C – прямоугольный с гипотенузой СA1.
Ответ: г.
Вариант 100
№2
Решение.
Площадь боковой поверхности конуса равна площади сектора.
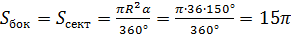 (см2).
(см2).
Ответ: г.
Вариант 104
№2
Решение.
Так как диаметр шара равен 18 см, то радиус шара равен 9 см. Если плоскость удалена от центра шара на расстояние, равное 8 см, то верно утверждение: плоскость пересекает шар.
Ответ: в.
Вариант 110
№2
Решение.
Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого равны образующим, а основание – диаметру конуса.
По неравенству треугольника получаем, что стороны равны 14,14 и 7 см.
Тогда радиус основания конуса равен 3,5 см.
Ответ: в.
Задание №3
Вариант 76
№3
Решение.
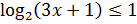 ;
;
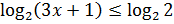 .
.
Так как  , то функция
, то функция 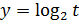 возрастает и неравенство равносильно системе неравенств
возрастает и неравенство равносильно системе неравенств 

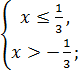
 .
.
 :
: 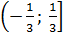 .
.
Вариант 87
№3
Решение.
 ;
; 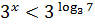 .
.
Так как  , то функция
, то функция 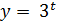 возрастает и неравенство равносильно неравенству
возрастает и неравенство равносильно неравенству 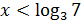 ;
; 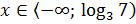 .
.
 :
: 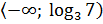 .
.
Вариант 101
№3
Решение.
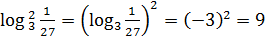 .
.
Ответ: 9.
Вариант 107
№3
Решение.
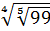 и
и  ;
;
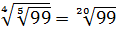 ;
;  .
.
Так как 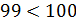 , то
, то  и
и 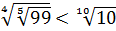 .
.
 :
: 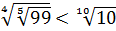 .
.
Вариант 122
№3
Решение.
 ;
;
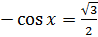 ;
;
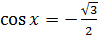 ;
;
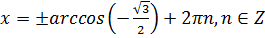 ;
;
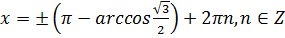 ;
;
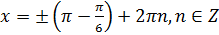 ;
;
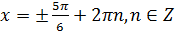 .
.
Ответ:  .
.
Вариант 94
№3
Решение.
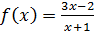 ;
; 
Найдем 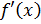 .
.
 .
.
Найдем  .
. 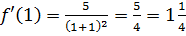 .
.
Ответ: 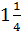 .
.
Задание №4
Вариант 81
№4
Решение.
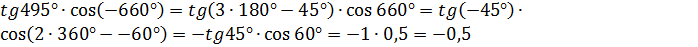 .
.
Ответ: -0,5.
Вариант 95
№4
Решение.
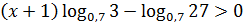 ;
;
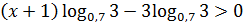 ;
;
 ;
;
 .
.
Так как  , то
, то  . Тогда
. Тогда 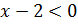 ;
;  ;
; 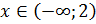 .
.
Наибольшее целое решение неравенства – число 1.
Ответ: 1.
Вариант 97
№4
Решение.
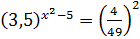 ;
;
 .
.
Так как степени с одинаковым основанием  равны, то равны и их показатели, т.е.
равны, то равны и их показатели, т.е.  ;
; 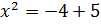 ;
; 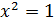 ;
; 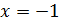 или
или 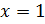 .
.
Ответ: -1 ; 1.
Вариант 119
№4
Решение.
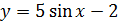 .
.
Так как  , то
, то 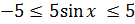 и
и  .
.
Значит, 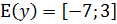 .
.
Ответ: 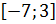 .
.
Вариант 127
№4
Решение.
Функция 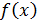 возрастает на множестве R. Значит, большему значению аргумента соответствует большее значение функции.
возрастает на множестве R. Значит, большему значению аргумента соответствует большее значение функции.
Сравним значения выражений  и
и  .
.
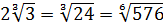 ;
; 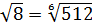 .
.
Так как 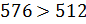 , то
, то 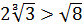 .
.
Из определения возрастающей функции следует, что 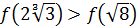 .
.
Ответ: 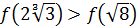 .
.
Задание №5
Вариант 118
№5
Решение.
 ,
,  .
.
Найдем абсциссу точки касания, составим и решим уравнение.
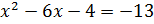 ;
;
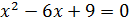 ;
;
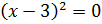 ;
;
 .
.

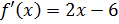 ;
; 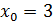 ;
;
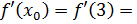 0;
0;
 .
.
Уравнение касательной имеет вид 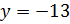 .
.
Ответ: 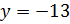 .
.
Вариант 122
№5
Решение.
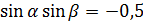 ,
, 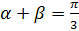 ,
, 
 ;
; 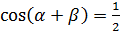 .
.
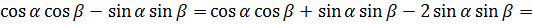

Получаем 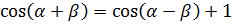 ;
; 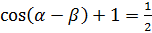 .
.
Тогда 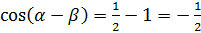 .
.
Ответ: 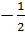 .
.
Вариант 130
№5
Решение.
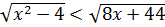 .
.
Неравенство равносильно системе неравенств
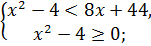
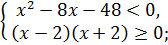

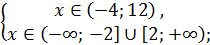
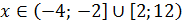 .
.
Ответ: 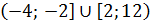 .
.
Вариант 132
№5
Решение.
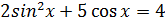 ;
;
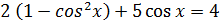 ;
;
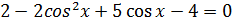 ;
;
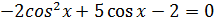 ;
;
 ;
;
Пусть  , тогда уравнение принимает вид
, тогда уравнение принимает вид 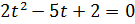 ;
;
 ;
; 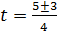 ;
;  .
.
 или
или 
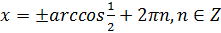 ; нет корней, так как
; нет корней, так как 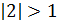 ;
;
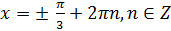 .
.
Ответ:  .
.
Вариант 138
№5
Решение.
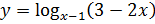 .
.
Для нахождения области определения функции составим и решим систему неравенств 
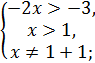
 ; значит,
; значит, 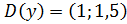 .
.
Ответ: 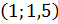 .
.
Задание №6
Вариант 76
№6
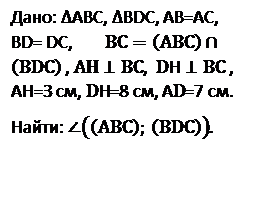

Решение.
1) Треугольники АВС и ВDС равнобедренные с общим основанием ВС, а так как 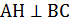 и
и 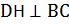 , то угол АНD является линейным углом двугранного угла DВСА, который равен углу между плоскостями АВС и ВDС. Значит, ∠
, то угол АНD является линейным углом двугранного угла DВСА, который равен углу между плоскостями АВС и ВDС. Значит, ∠  .
.
2) Рассмотрим треугольник  .
.
По теореме косинусов  ,
,
тогда
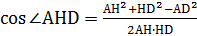 ;
;
 .
.
Так как  , то
, то 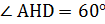 .
.
Значит, угол между плоскостями АВС и ВDС равен  .
.
Ответ:  .
.
Вариант 88
№6

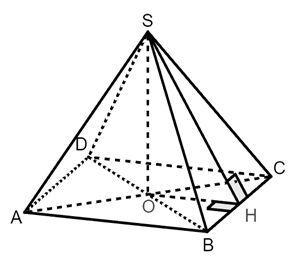 Решение.
Решение.
1) Пусть SО – высота пирамиды SABCD. Так как все боковые грани пирамиды равнонаклонены к плоскости основания, то основание высоты пирамиды точка О – центр окружности, вписанной в основание пирамиды. ABCD – ромб, О – точка пересечения диагоналей ромба.
2) Проведем ОН 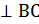 , соединим точки S и Н.
, соединим точки S и Н.
SО – перпендикуляр к плоскости АВС, SН – наклонная на плоскость АВС, ОН- проекция наклонной SН на плоскость АВС, ВС – прямая в плоскости АВС. Так как
ОН 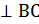 (по построению), то SН
(по построению), то SН 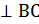 по теореме о трех перпендикулярах. Тогда
по теореме о трех перпендикулярах. Тогда
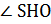 – линейный угол двугранного угла SВСО, т.е.
– линейный угол двугранного угла SВСО, т.е. 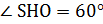 .
.
3) Пусть сторона ромба равна 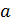 см, а высота ромба -
см, а высота ромба - 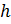 см.
см.
Тогда  или
или  .
.
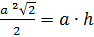 ;
;  . По свойству ромба
. По свойству ромба 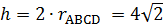 (см), тогда
(см), тогда
 (см).
(см).
4) Рассмотрим треугольник 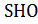 : ∠
: ∠ 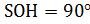 ,
, 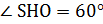 , тогда
, тогда 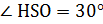 и
и
 (см).
(см).
Так как все боковые грани пирамиды равнонаклонены к плоскости основания, высоты боковых граней, проведенные к сторонам основания равны. SН – высота боковой грани пирамиды. Тогда площадь боковой поверхности можно найти по формуле 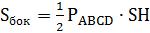 .
.
 (см2).
(см2).
Ответ: 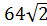 см2.
см2.
Вариант 92
№6
 |
 Решение.
Решение.
1) В результате вращения равнобедренного прямоугольного треугольника АВС вокруг гипотенузы АВ получим тело вращения, состоящее из двух равных конусов с общим основанием, радиус которых равен высоте треугольника, проведенной к гипотенузе АВ, а высота конусов равна половине гипотенузы.
2) Пусть 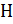 – высота,
– высота,  – радиус каждого конуса,
– радиус каждого конуса, 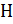 =
=  ,
, 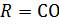 .
.
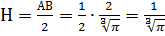 (см);
(см); 
Рассмотрим треугольник ВОС, ∠  ,
, 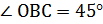 , тогда
, тогда 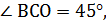 значит, треугольник ВОС прямоугольный и равнобедренный,
значит, треугольник ВОС прямоугольный и равнобедренный, 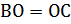 .
.
Тогда 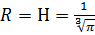 см.
см.
3) Найдем объем полученного тела вращения.
 (см2).
(см2).
Ответ:  см2.
см2.
Вариант 102
№6
 Решение.
Решение.
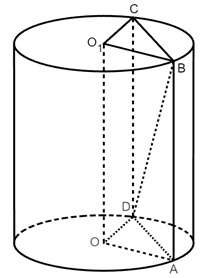
1) Так как градусная мера дуги равна градусной мере соответствующего центрального угла, то 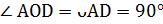 . Рассмотрим треугольник
. Рассмотрим треугольник 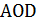 :
: 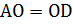 (как радиусы основания цилиндра), значит, он прямоугольный и равнобедренный. По теореме Пифагора
(как радиусы основания цилиндра), значит, он прямоугольный и равнобедренный. По теореме Пифагора 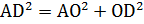 ;
; 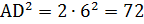 ;
;
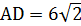 см.
см.
2) Сечение цилиндра, параллельное оси – прямоугольник ABCD, AB – образующая цилиндра, AB=  . Рассмотрим треугольник ABD :
. Рассмотрим треугольник ABD : 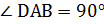 , BD=
, BD= 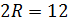 см (по условию),
см (по условию), 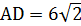 см. По теореме Пифагора
см. По теореме Пифагора 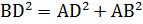 , откуда
, откуда 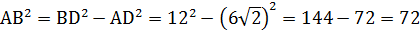 ;
; 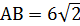 см.
см.
3) 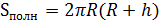 ,
,  см, тогда
см, тогда
 (см2).
(см2).
Ответ: 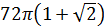 см2.
см2.
Вариант 104
№6

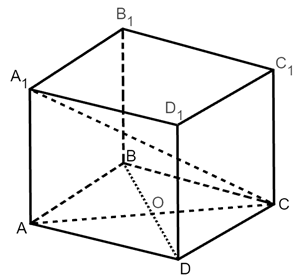
Решение.
1) Так как параллелепипед прямой, то его боковые грани прямоугольники. Тогда АВ 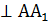 и А
и А 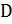
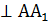 и ∠
и ∠  является линейным углом двугранного угла при ребре
является линейным углом двугранного угла при ребре 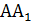 , ∠
, ∠ 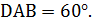
2) Найдем площадь основания параллелепипеда. ABCD – ромб,
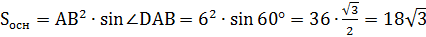 (см2).
(см2).
3) В ромбе ABCD ∠ 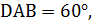 тогда ∠
тогда ∠  , следовательно, BD
, следовательно, BD  АС. BD и АС ортогональные проекции диагоналей
АС. BD и АС ортогональные проекции диагоналей 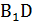 и
и 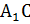 на плоскость основания параллелепипеда. По свойству наклонных и проекций
на плоскость основания параллелепипеда. По свойству наклонных и проекций  , значит,
, значит, 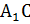 – большая диагональ параллелепипеда. По теореме косинусов из треугольника АВС найдем длину диагонали АС.
– большая диагональ параллелепипеда. По теореме косинусов из треугольника АВС найдем длину диагонали АС.
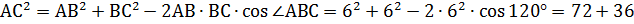 ;
;
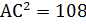 ;
; 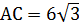 см.
см.
Рассмотрим треугольник 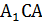 (∠
(∠ 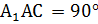 ). По условию ∠
). По условию ∠  , тогда
, тогда
∠  треугольник является равнобедренным с основанием
треугольник является равнобедренным с основанием 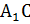 . Значит,
. Значит, 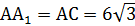 см.
см.
4) 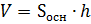 ; так как в прямом параллелепипеде высота равна боковому ребру, то
; так как в прямом параллелепипеде высота равна боковому ребру, то 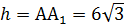 см;
см; 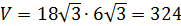 (см2).
(см2).
Ответ: 324 см2.
Вариант 138
№6

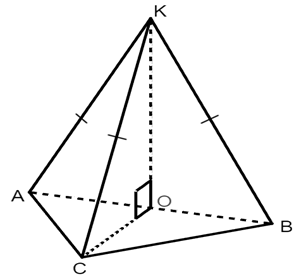
Решение.
1) Соединим точку К с вершинами треугольники АВС, проведем перпендикуляр на плоскость АВС из точки К. Рассмотрим треугольники АКО, СКО и ВКО. Так как 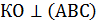 , а отрезки АО, ВО и СО лежат в плоскости, то треугольники прямоугольные. КА=КС=КВ (по условию), КО – общая сторона. Следовательно треугольники равны по гипотенузе и катету. Из равенства треугольников следует, что АО=ВО=СО, т.е. о – центр окружности, описанной около треугольника АВС. Так как треугольник АВС прямоугольный, то О – середина гипотенузы.
, а отрезки АО, ВО и СО лежат в плоскости, то треугольники прямоугольные. КА=КС=КВ (по условию), КО – общая сторона. Следовательно треугольники равны по гипотенузе и катету. Из равенства треугольников следует, что АО=ВО=СО, т.е. о – центр окружности, описанной около треугольника АВС. Так как треугольник АВС прямоугольный, то О – середина гипотенузы.
АО=ВО=СО= 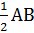 =5(см).
=5(см).
2) КС - наклонная на плоскость АВС, КО – перпендикуляр к плоскости АВС, СО – проекция наклонной КС на плоскость АВС. По определению угла между прямой и плоскостью ∠ 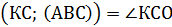 .
.
3) Рассмотрим треугольник КСО ( 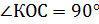 ). СО=5 см, КС=20 см.
). СО=5 см, КС=20 см.
Тогда  и
и  .
.
Значит, угол между прямой КС и плоскостью АВС равен 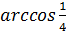 .
.
Ответ: 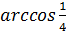 .
.
Задание №7
Вариант 72
№7
Решение.
Найдем производную функции 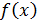 :
:
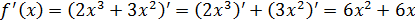 .
.
Согласно геометрическому смыслу производной 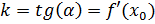 .
.
Так как касательные параллельны оси Ox, то 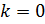 ;
;
Значит,  ;
;
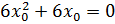 ;
;
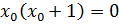 ;
;
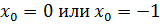 ;
;
Значит, 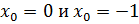 являются абсциссами точек касания.
являются абсциссами точек касания.
Уравнение касательной к графику в точке с абсциссой 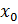 :
: 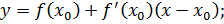
1. При 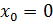 имеем
имеем
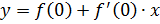 ;
;
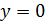 .
.
2. При  имеем
имеем
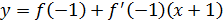 ;
;
 ;
;
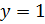 .
.
Ответ: 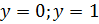 .
.
Вариант 83
№7
Решение.
Прямая 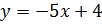 является касательной к графику функции
является касательной к графику функции  .
.
Согласно геометрическому смыслу производной 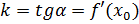 .
.
Угловой коэффициент касательной 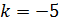 ;
;
найдем производную функции: 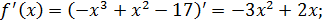
Пусть 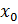 – абсцисса точки касания. Составим и решим уравнение
– абсцисса точки касания. Составим и решим уравнение
 ;
;
 ;
;
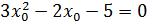 ;
;
 ;
;
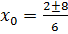 ;
;
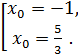
Ответ: 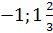 .
.
Вариант 114
№7
Решение.
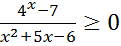
Решим неравенство методом интервалов.
Рассмотрим функцию 
Область определения функции: 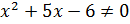
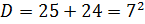
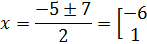

Нули функции: 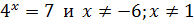
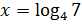 – нуль функции.
– нуль функции.

(на рисунке  обозначен как log(4, 7))
обозначен как log(4, 7))
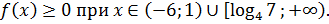
Ответ: 
Вариант 126
№7
Решение.

Вычислим 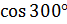 .
.
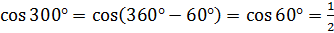 ;
;
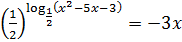 ;
;
Уравнение равносильно системе
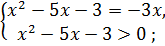
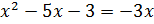 ;
;
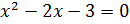 ;
;
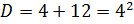 ;
;
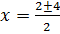 ;
;
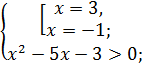
При 
 ; при
; при 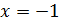
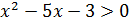 .
.
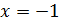 - корень уравнения.
- корень уравнения.
Ответ: 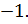
Вариант 134
№7
Решение.
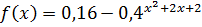 ;
; 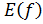 -?
-?
Рассмотрим функцию  и найдем ее область значений.
и найдем ее область значений.
Это квадратичная функция, ее график парабола, ветви которой направлены вверх.
Найдем координаты вершины: 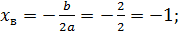
 ;
;
Так как ветви параболы направлены вверх, то 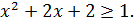
Так как 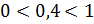 , то показательная функция
, то показательная функция  убывает, значит,
убывает, значит,
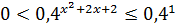 ;
;
 ;
;
 ;
;
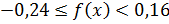 :
:
Значит, 
Ответ: 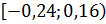 .
.
Задание №8
Вариант 78
№8
Решение.
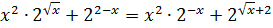 ;
;
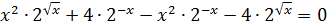 .
.
Разложим на множители левую часть уравнения:
 ;
;
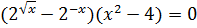 .
.
Произведение двух множителей равно нулю, тогда и только тогда, когда один из множителей равен нулю, а другой существует, значит:
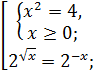
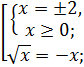
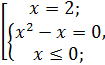
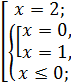

Ответ: 0; 2.
Вариант 88
№8
Решение.
 .
.
Естественная область определения уравнения: 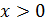
Т.к. обе части уравнения положительны, то прологарифмируем обе части уравнения по основанию 3:
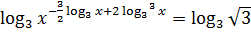 ;
;
 ;
;
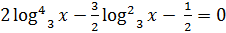 ;
;
 .
.
Пусть 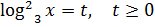 , тогда уравнение принимает вид
, тогда уравнение принимает вид 
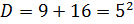
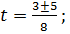
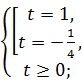
 .
.
Тогда
 ;
;
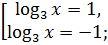
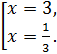
Ответ: 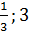 .
.
Вариант 96
№8
Решение.
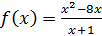 .
.
Найдем область определения функции: 
Найдем производную функции.
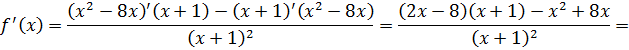
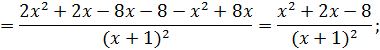
Найдем нули производной: 


Функция 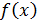 убывает на промежутках
убывает на промежутках 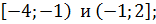
функция 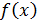 возрастает на промежутках
возрастает на промежутках 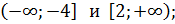
точка минимума: 
точка максимума: 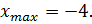
Ответ: функция убывает на промежутках 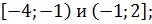
функция возрастает на промежутках 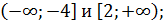

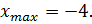
Вариант 106
№8
Решение.
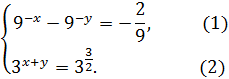
Рассмотрим уравнение 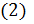 системы:
системы:
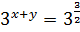 ;
;
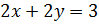 ;
;
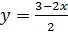 .
.
Подставим выражение 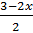 вместо
вместо 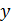 в уравнение
в уравнение  .
.

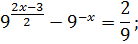

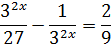
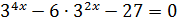
Пусть 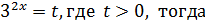 уравнение принимает вид
уравнение принимает вид
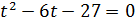
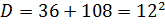
 ;
; 
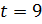 .
.
 ;
;
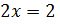 ;
;
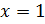 ;
;
тогда 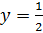 .
.
Ответ:  .
.
Вариант 112
№8
Решение.
 ;
;
Пусть  – точка пересечения графика функции
– точка пересечения графика функции 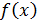 с осью ординат,
с осью ординат,
тогда 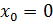 , а
, а 
Найдем производную функции 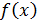 и ее значение при
и ее значение при 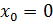 .
.
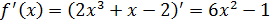 ;
;
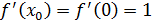 .
.
Согласно геометрическому смыслу производной 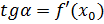 .
.
Значит,  ;
;  .
.
Ответ: 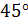 .
.
Вариант 118
№8
Решение.
 ;
;
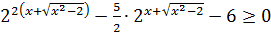 ;
;
 ;
;
Пусть 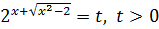 ,
, 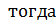 неравенство принимает вид
неравенство принимает вид 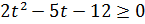 .
.
Решим неравенство методом интервалов.
 ;
;
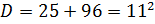 ;
;
 ;
;  ,
, 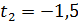 .
.


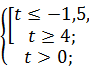 значит,
значит, 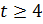 .
.
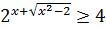 ;
;
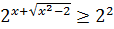 ;
;
Так как  , то показательная функция
, то показательная функция  возрастает,
возрастает,
значит, 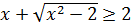 ;
;
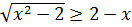 ;
;

Решим систему неравенств (1):
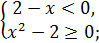

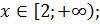
Решим систему неравенств (2):
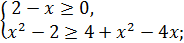

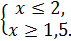
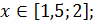
Объединив решения систем, получаем решение исходного неравенства 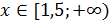 .
.
Ответ: 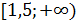 .
.
Задание №9
Вариант 84
№9
Решение.
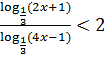 .
.
Заметим, что в левой части неравенства можно применить формулу перехода к новому основанию логарифма:
 .
.
Получаем неравенство 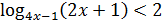 ;
;
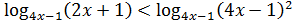 .
.
Рассмотрим два случая:
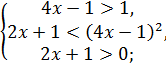 или или 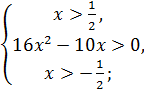   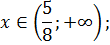
| 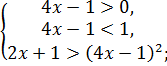 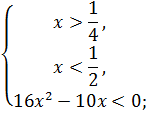 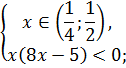 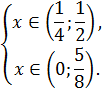 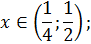
|
Объединим решения систем неравенств и получим: 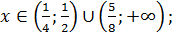
Ответ: 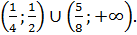
Вариант 87
№9
Решение.
Пусть 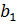 - первый член данной прогрессии,
- первый член данной прогрессии, 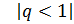
 - знаменатель прогрессии,
- знаменатель прогрессии,  .
.
Тогда сумма прогрессии равна
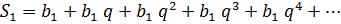 или по формуле суммы бесконечно убывающей геометрической прогрессии
или по формуле суммы бесконечно убывающей геометрической прогрессии 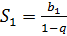 .
.
Квадраты членов данной прогрессии 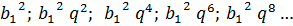 образуют новую бесконечно убывающую геометрическую прогрессию, первый член которой равен
образуют новую бесконечно убывающую геометрическую прогрессию, первый член которой равен  , а знаменатель прогрессии равен
, а знаменатель прогрессии равен  . Тогда сумма новой прогрессии
. Тогда сумма новой прогрессии  .
.
Составим и решим систему уравнений: 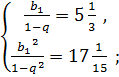
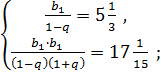
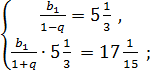

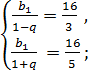
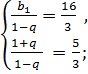
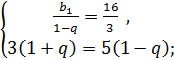
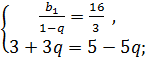

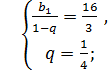
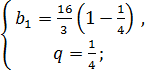

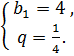
Ответ: 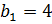 ;
;  .
.
Вариант 97
№9
Решение.
 , значит, график функции
, значит, график функции 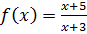 не проходит через точку с координатами (0; 0).
не проходит через точку с координатами (0; 0).
Найдем производную функции
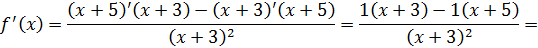
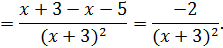
Пусть 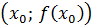 общая точка графика функции и касательной, тогда
общая точка графика функции и касательной, тогда
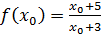 ;
; 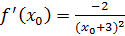 .
.
Запишем уравнение касательной:
 ;
;  .
.
Так как касательная проходит через начало координат, то в уравнение касательной можно подставить 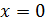 ,
, 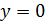 , получаем
, получаем 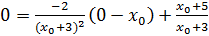 .
.
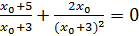 ;
; 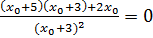 ;
;  ;
;