
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формула Стокса
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливается формулой Стокса.
Теорема. Если функции X(x,y,z), Y(x,y,z), Z(x,y,z) непрерывна вместе со своими частными производными первого порядка во всех точках ориентированной поверхности S, то имеет место формула:
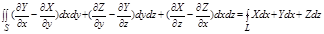
 где L–граница поверхности S, интегрируемая в положительном направления.
где L–граница поверхности S, интегрируемая в положительном направления.
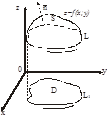
Доказательство: Пусть z=f(x,y) уравнение поверхности S правильной в направлении оси Oz функции 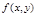 ,
, 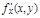 и
и 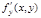 непрерывны в замкнутой области
непрерывны в замкнутой области 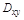 (проекции поверхности S на плоскость xOy),
(проекции поверхности S на плоскость xOy), 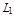 – граница область D.
– граница область D.
Рассмотрим интеграл
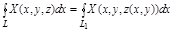
т.к. значение функции X(x,y,z) на L равны значениям X(x,y,z(x,y)) на 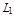 , то применим формулу Остроградского – Грина.
, то применим формулу Остроградского – Грина.
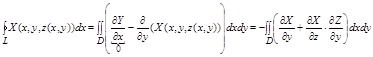
Преобразуем полученный двойной интеграл в интеграл по поверхности II рода.
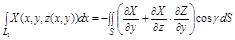
Так как выбрана верхняя сторона поверхности, то 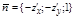 , а направляющиеся косинусы пропорциональны соответствующим координатам (проекциям) вектора нормали
, а направляющиеся косинусы пропорциональны соответствующим координатам (проекциям) вектора нормали
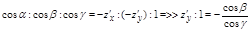
Тогда
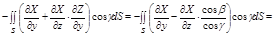
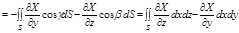
Следовательно 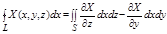
Аналогично получим
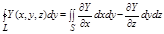
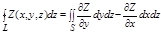
Сложив полученные равенства почленно, мы получим формулу Стокса.
Замечание:
Из формулы Стокса вытекает, что если выполняются равенства:
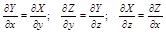
то криволинейный интеграл по замкнутой пространственной кривой L равен нулю
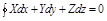
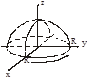 Пример. Вычислить
Пример. Вычислить 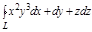 , где L: окружность
, где L: окружность 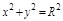 ,
, 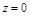
1. Рассмотрим в качестве поверхности натянутой на контур полусферу 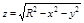 , нормаль внешняя.
, нормаль внешняя.
2. 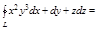
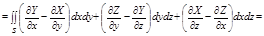
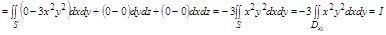
Для удобства вычислений перейдем к полярной системе координат:
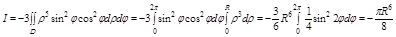
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|