
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема урока: Решение рациональных и показательных уравнений.
Тема урока: Решение рациональных и показательных уравнений.
Алгебра возникла из решения практических задач с помощью уравнений. Цели алгебры оставались неизменными на протяжении тысячелетий- решались уравнения: сначала линейные, потом квадратные, а там и уравнения еще больших степеней. Но форма, в которой излагались алгебраические результаты, менялись до неузнаваемости.
Уравнение- это самая распространенная форма математической задачи. Учение об уравнениях является главным содержанием школьного курса алгебры. Для решения уравнений нужно уметь производить действия над одночленами, многочленами алгебраическими дробями, уметь производить разложение на множители, раскрывать скобки и т. д. Нужно привести свои знания в порядок. Мы начнем повторение с понятия «рациональные выражения». Сообщение ученика о рациональных выражениях известных из основной школы. Таким образом, учение об уравнениях невозможно без учения о законах действий.
II. Основная часть.
Главное в понятии уравнения – это постановка вопроса о его решении. Уравнение, левая и правая части которого есть рациональные выражения относительно х, называют рациональным уравнением с неизвестным х.
Например, уравнения 5х6 - 9х5 + 4х - Зх + 1 = 0, 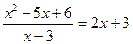 являются рациональными.
являются рациональными.
Корнем (или решением) уравнения с неизвестным х называют число, при подстановке которого в уравнение вместо х получается верное числовое равенство.
Решить уравнение — значит найти все его корни или показать, что их нет. При решении рациональных уравнений приходится умножать и делить обе части уравнения на не равное нулю число, переносить члены уравнения из одной части в другую, применять правила сложения и вычитания алгебраических дробей. В результате будет получаться уравнение, равносильное предшествующему, т. е. уравнение, имеющее те же корни, и только их.
Перечислим стандартные уравнения, которые были нами изучены. Ответы учащихся.( линейное уравнение , квадратное уравнение, простейшее степенное уравнение хn=а). Преобразование уравнений к одному из стандартных является основным шагом в решении уравнения. Полностью алгоритмизировать процесс преобразования нельзя, однако полезно запомнить некоторые приемы, общие для всех типов уравнений.
1).Уравнение вида А(х)•В(х) = О, где А(х) и В(х) — многочлены относительно х, называют распадающимся уравнением.
Множество всех корней распадающегося уравнения есть объединение множеств всех корней двух уравнений А(х)=0 и В(х)=0. К уравнениям вида А(х)=0 применяется метод разложения на множители. Суть этого метода : нужно решить уравнение А(х)=0, где А(х)=А1(х)А2(х)А3(х). Уравнение А(х)=0 заменяют совокупностью простых уравнений: А1(х)=0,А2(х)=0,А3(х)=0. Находят корни уравнений этой совокупности и делают проверку. Метод разложения на множители используется в основном для рациональных и тригонометрических уравнений.
ПРИМЕР 1.
Решим уравнение (х2 - 5х + 6) (х2 + х - 2) = 0.
Уравнение распадается на два уравнения.
х2 - 5х + 6 = 0 х1 = 2 и х2 = 3
х2 + х - 2 = 0. х3 = -2 и х4 = 1
Значит, уравнение исходное имеет корни х1= 2, х2 = 3, х3= -2, х4 =1.
Ответ. -2; 1; 2; 3.
ПРИМЕР. Решим уравнение х3-7х+6=0.
х3-х-6х+6=0
х(х2-1)-6(х-1)=0
х(х-1)(х+1)-6(х-1)=0
(х-1)(х(х+1)-6)=0
(х-1)(х2+х-6)=0
х-1=0 , х1=1; х2+х-6=0, х2=2,х3=-3.
Ответ:1;2;-3.
2).Уравнение вида 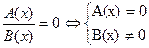 , где А(х) и В(х) — многочлены относительно х.
, где А(х) и В(х) — многочлены относительно х.
ПРИМЕР 2.
Решим уравнение 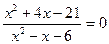
Сначала решим уравнение
х2 + 4х - 21 = 0. х1 = 3 и х2 = -7
Подставив эти числа в знаменатель левой части исходного уравнения, получим
х1 2- х1 -6 = 9-3-6 = 0,
х2 2- х2 - 6 = 49 + 7 - 6 = 50 ≠0.
Это показывает, что число х1 = 3 не является корнем исходного уравнения, а число х2 =- 7 — корень этого уравнения.
Ответ. -7.
3).Уравнение вида
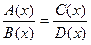
где А(х), В(х), С(х) и D(х) — многочлены относительно х, обычно решают по следующему правилу.

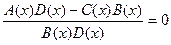
Решают уравнение А(х)•D(х) - С(х)·В(х) = 0 и отбирают из его корней те, которые не обращают в нуль знаменатель уравнения.
ПРИМЕР 3.
Решим уравнение
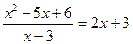
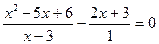
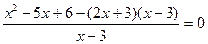
Решим уравнение
х2 - 5х + 6 - (2х + 3) (х - 3) = 0.
х2 + 2х - 15 = 0
х1 = -5 и х2 = 3.
Число х1 не обращает в нуль знаменатель х - 3, а число х2 обращает. Следовательно, уравнение имеет единственный корень = -5.
Ответ. -5.
Д/З
1. Найти корни целого уравнения
3⋅(x+1)⋅(x−3)= x(2x−1)−3
2 Решите уравнение 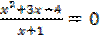
Уравнение, в котором неизвестное содержится в показателе степени, считается показательным (слайд № 4). Рассмотрим основные виды показательных уравнений (слайд № 5) (учащиеся записывают названия видов и примеры в тетрадях).
1. Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида ах = ав, где а >0, а ≠ 1. При этом используется свойство степени, которое мы изучали (повторить следствие 2 на стр. 160 учебника). Рассмотрим примеры решения таких уравнений.
Пример 1 (слайд № 6).
(0,0016)0,2 х + 1 = 25;
5 – 4 (0,2 х + 1) = 52;
– 0,8 х – 4 = 2;
– 0,8 х = 6;
х = – 7,5 .
Ответ: – 7,5.
Пример 2 (слайд №7)
36 · 6х = 1;
62 + х = 60;
2 + х = 0;
х = – 2.
Ответ: – 2.
Пример 3 (слайд №8)
81х · 24х = 36;
34х · 24х = 62;
64х = 62;
4х = 2;
х = 0,5.
Ответ: 0,5.
Пример 4 (слайд № 9)
2х – 3 = 3х – 3;
х – 3 = 0;
х = 3.
Ответ: 3.
2. Вынесение общего множителя за скобки (слайд № 10). Рассмотрим примеры решения таких уравнений.
Пример 1.
2 · 3х + 1 – 6 · 3х – 1 – 3х = 9;
3х(2 · 3 – 6 · 3– 1 – 1) = 9;
3х · 3 = 9;
3х = 3;
х = 1.
Ответ: 1
Пример 2 (слайд № 11).
52х – 7х – 52х · 17 + 7х · 17 = 0;
52х – 52х · 17 = 7х – 7х · 17;
52х(1 – 17) = 7х(1 – 17);
– 16· 52х = – 16 · 7х;
52х = 7х;
25х = 7х;
х= 0.
Ответ: 0.
3. Сведение к квадратному уравнению (слайд № 12). Рассмотрим примеры решения таких уравнений.
Пример:
9х – 4 · 3х = 45;
32х – 4 · 3х – 45 = 0;
Замена 3х = t, t > 0;
t2 – 4 t – 45 = 0;
D = 16 +180 = 196;
t1 = 9,
t2 = – 5 – не удовлетворяет условию t > 0;
3х = 9;
3х = 32;
х = 2;
Ответ: 2.
Д/З
Найдите корень уравнения 
3x – 3x – 2 = 24
22x + 2x– 12 = 0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|